Вычислите S=2/(4∙2!)+2/(5∙3!)+2/(6∙4!)+2/(7∙5!)+2/(8∙6!)+⋯. - вопрос №24225326427528613593210 от Женя220V 24.04.2021 01:16

Question

Алгебра: Вычислите S=2/(4∙2!)+2/(5∙3!)+2/(6∙4!)+2/(7∙5!)+2/(8∙6!)+⋯.

Женя220V · Answer

Сразу вынесем 2 за скобку. Считаем сумму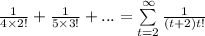 , причем легко показать, что эта сумма сходится. Действительно, эта сумма меньше, чем 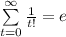. Перепишем общий член нашей суммы: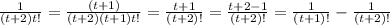 . Имеем: ....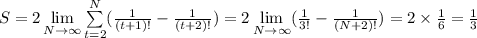