Видим, что Григорий получал оценку «уд.» в начале года, что говорит о том, что он многое не понимал и не мог выполнить. Однако в ноябре-декабре оценка уже переходит порог «хорошо». Таким образом, делаем вывод, что студент очень старательный, ведь в задаче явно сказано, что никакого математического образования у него нет, но при этом у него получилось к концу года стабильно получать «хорошо» и «отлично» по данной дисциплине. В январе чаще всего у студентов каникулы и сессия, поэтому Григорий, получив на экзамене отличную оценку, которая, будучи единственной в этом месяце, сформировала средний , отправился на заслуженный отдых.
1)
а) (a+3)(b-7) = ab - 7a + 3b -21
б) (a-5)(11-b) = 11a - ab - 55 + 5b
в) (-8-a)(b+2) = -8b - 16 - ab - 2a
г) (-7-b)(a-7) = -7a + 49 - ab + 7b
2)
а) (x-4)(x+8) =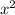
+ 4x - 32
б) (x-5)(9-x) = -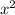
+ 14x - 45
в) (3+x)(-1-x) =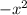
- 4x - 3
г) (x - 10)(-x-6) =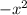
+ 4x + 60
3)
а) (8+3x)(2y-1) = 16y - 8 + 6xy - 3x
б) (2a-1)(3a+7) = 6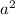
+ 11a - 7
в) (3a-2b)(2a-3b) =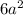
- 13ab + 6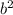
г) (15a+27)(-5a-9) =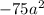
- 270a - 243
4)
а) (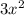
-1)(2x+1) = 
+ 
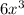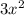- 2x - 1
б) (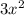
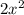-1)(
+1) =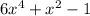 
в) (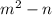
)(
) = 
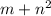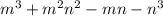
г) (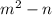
)(
) = 
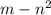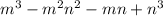
5)
а) (a+2)(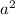
- a - 3) =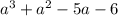 
б) (5b-1)(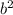
-5b+1) =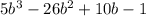 
в) (m-n+1)(m+n) =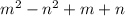
г) (m-2n)(m+2n-1) =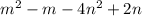
6)
а) 2(b+1)(b+3) =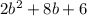
б) -8(y-1)(y+5) =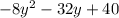
в) b(3b+1)(2b-5) =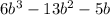
г) 5m(m-n)(m+3n) =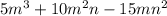
Объяснение:
+79771935114 Qiwi
Объяснение:
Видим, что Григорий получал оценку «уд.» в начале года, что говорит о том, что он многое не понимал и не мог выполнить. Однако в ноябре-декабре оценка уже переходит порог «хорошо». Таким образом, делаем вывод, что студент очень старательный, ведь в задаче явно сказано, что никакого математического образования у него нет, но при этом у него получилось к концу года стабильно получать «хорошо» и «отлично» по данной дисциплине. В январе чаще всего у студентов каникулы и сессия, поэтому Григорий, получив на экзамене отличную оценку, которая, будучи единственной в этом месяце, сформировала средний , отправился на заслуженный отдых.