Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
- координата вершины
z = 0 - координата вершины параболы
x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
Объяснение:
a = 1 (коэффициент при x^2)
b = 6 (коэффициент при x)
c = -5 (свободный элемент)
1) Вершина параболы находится по формуле
xв = -b/2a = -6/(2*1) = -3
yв находится подстановкой хв в исходное уравнение
ув = () + 6 *(-3) -5 = 9 -18 - 5 = -14
Координаты точки вершины (-3, -14)
2) Пересечение с ОХ происходит когда y = 0
+ 6x - 5 = 0
D = 36 + 5*4 = 56
Тогда пересечение с осью ОХ происходит в точках:
x1 =
x2 =
3) Пересечение с ОУ происходит когда x = 0
y = 0 + 0 -5 = -5
(0, -5)
4) x = m
y = 3
3 =
- 6m - 8 = 0
D = 36 + 32 = 68
m1 =
m2 =
5)
Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
Объяснение:
a = 1 (коэффициент при x^2)
b = 6 (коэффициент при x)
c = -5 (свободный элемент)
1) Вершина параболы находится по формуле
xв = -b/2a = -6/(2*1) = -3
yв находится подстановкой хв в исходное уравнение
ув = (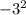 ) + 6 *(-3) -5 = 9 -18 - 5 = -14
) + 6 *(-3) -5 = 9 -18 - 5 = -14
Координаты точки вершины (-3, -14)
2) Пересечение с ОХ происходит когда y = 0
D = 36 + 5*4 = 56
Тогда пересечение с осью ОХ происходит в точках:
x1 =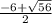
x2 =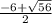
3) Пересечение с ОУ происходит когда x = 0
y = 0 + 0 -5 = -5
(0, -5)
4) x = m
y = 3
3 =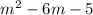
D = 36 + 32 = 68
m1 =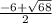
m2 =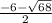
5)