Здесь правая часть уравнения зависит только от переменной у. Вводим замену тогда , получаем
- уравнение с разделяющимися переменными
Выполним обратную замену
Последний интеграл не так уж и просто вычислить...
Здесь правая часть уравнения зависит только от переменной у. Вводим замену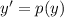 тогда
тогда 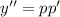 , получаем
, получаем
Выполним обратную замену
Последний интеграл не так уж и просто вычислить...