Является ли решением уравнения 6х+у=4 пара чисел (-2; 16), (4; -10), (-0,5; 8), (-3;14), (1;-2)? №2. Из линейного уравнения 2х+4у=8 а) выразите X через Y; б) выразите Y через X.
№2. Из линейного уравнения 2х+4у=8 а) выразите X через Y; б) выразите Y через X .
Выполнить в тетради построение графика уравнения: а) 3х+у=6 ; б)2х+у=0; в)4,5х=-9 ; г)2у=10; д ) 0,5х-у=1; е) 2,6х+2у=4.

Напишите ответ очень надо

Показать ответ

Ответ:

31Maks31

29.08.2022 03:56

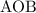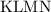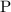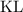Пусть в сектор $\mathrm{AOB}$ вписан прямоугольник $\mathrm{KLMN}$ . $\mathrm{P}$ и $\mathrm{Q}$ - середины сторон $\mathrm{KL}$ и $\mathrm{MN}$ соответственно. Так как прямоугольник симметричен оси симметрии сектора, то две его стороны перпендикулярны этой оси, а две другие стороны - параллельны этой оси.

Так как прямоугольник симметричен оси симметрии сектора, то:

$\mathrm{\angle\ AOC=\angle\ BOC=\alpha}$

Проведем луч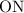 $\mathrm{ON}$ , составляющий с осью симметрии сектора угол . Зададим ограничения на х: $x\in[0;\ \alpha ]$

Найдем сторону прямоугольника, перпендикулярную оси симметрии сектора.

Рассмотрим треугольник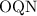 $\mathrm{OQN}$ . Запишем соотношение для синуса угла х:

$\sin x=\mathrm{\dfrac{QN}{ON}}$

Заметим, что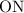 $\mathrm{ON}$ соответствует радиусу сектора. Тогда, выражение для 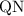$\mathrm{QN}$ примет вид:

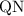$\mathrm{QN}=R\cdot\sin x$

Так как $\mathrm{QN}$ - половина стороны $\mathrm{MN}$ , то найдена первая сторона прямоугольника:

$\mathrm{MN}=2R\cdot\sin x$

Найдем сторону прямоугольника, параллельную оси симметрии сектора. Представим ее длину в виде:

$\mathrm{LM=KN=PQ=OQ-OP}$

Длину найдем из того же прямоугольного треугольника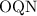 $\mathrm{OQN}$ , записав выражение для косинуса угла :

$\cos x=\mathrm{\dfrac{OQ}{ON}}$

Выражаем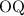 $\mathrm{OQ}$ :

$\mathrm{OQ}=R\cdot \cos x$

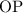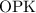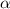Длину $\mathrm{OP}$ найдем из прямоугольного треугольника $\mathrm{OPK}$ . Запишем выражение для тангенса угла $\alpha$ :

$\mathrm{tg}\alpha =\mathrm{\dfrac{PK}{OP} }$

Откуда:

$\mathrm{OP=\dfrac{PK}{\mathrm{tg}\alpha} }$

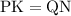Так как $\mathrm{PK=QN}$ , то:

$\mathrm{OP}=\dfrac{R\cdot\sin x}{\mathrm{tg}\alpha}$

Таким образом, найдена вторая сторона прямоугольника:

$\mathrm{LM}=R\cdot \cos x-\dfrac{R\cdot\sin x}{\mathrm{tg}\alpha}$

Площадь прямоугольника равна произведению его смежных сторон:

$S=\mathrm{MN\cdot LM}$

$S=2R\cdot\sin x\cdot\left(R\cdot \cos x-\dfrac{R\cdot\sin x}{\mathrm{tg}\alpha}\right)=2R^2\cdot\sin x\cdot\left( \cos x-\dfrac{\sin x}{\mathrm{tg}\alpha}\right)$

Найдем производную:

$S'=2R^2\cdot(\sin x)'\cdot\left( \cos x-\dfrac{\sin x}{\mathrm{tg}\alpha}\right)+2R^2\cdot\sin x\cdot\left( \cos x-\dfrac{\sin x}{\mathrm{tg}\alpha}\right)'$

$S'=2R^2\cdot\cos x\cdot\left( \cos x-\dfrac{\sin x}{\mathrm{tg}\alpha}\right)+2R^2\cdot\sin x\cdot\left(-\sin x-\dfrac{\cos x}{\mathrm{tg}\alpha}\right)$

$S'=2R^2\cdot\left( \cos^2 x-\dfrac{\sin x\cos x}{\mathrm{tg}\alpha}-\sin^2 x-\dfrac{\sin x\cos x}{\mathrm{tg}\alpha}\right)$

$S'=2R^2\cdot\left( \cos^2 x-\sin^2 x-\dfrac{2\sin x\cos x}{\mathrm{tg}\alpha}\right)$

$S'=2R^2\cdot\left( \cos2x-\dfrac{\sin 2x}{\mathrm{tg}\alpha}\right)$

Приравняем производную к нулю:

$2R^2\cdot\left( \cos2x-\dfrac{\sin 2x}{\mathrm{tg}\alpha}\right)=0$

$\cos2x-\dfrac{\sin 2x}{\mathrm{tg}\alpha }=0$

$\dfrac{\sin 2x}{\mathrm{tg}\alpha }= \cos2x$

$\sin 2x= \cos2x\mathrm{tg}\alpha$

$\mathrm{tg}2x= \mathrm{tg}\alpha$

Учитывая ограничения $x\in[0;\ \alpha ]$ получим, что:

$x=\dfrac{\alpha }{2}$

Проверим, является ли эта точка точкой экстремума.

Найдем значение производной при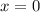 x=0 :

$S'=2R^2\cdot\left( \cos0-\dfrac{\sin 0}{\mathrm{tg}\alpha}\right)=2R^2\cdot\left( 1-0\right)=2R^2$

Найдем значение производной при $x=\alpha$ :

$S'=2R^2\cdot\left( \cos2\alpha -\dfrac{\sin 2\alpha }{\mathrm{tg}\alpha}\right)=2R^2\cdot\left( \cos2\alpha -\dfrac{2\sin \alpha \cos^2\alpha }{\sin\alpha}\right)=$

$=2R^2\cdot\left( 2\cos^2\alpha-1 -2\cos^2\alpha \right)=2R^2\cdot\left( -1 \right)=-2R^2$

При переходе через точку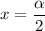 $x=\dfrac{\alpha }{2}$ производная меняет знак с плюса на минус. Значит, это точка максимума.

Найдем значение максимума:

$S\left(\dfrac{\alpha }{2}\right)=2R^2\cdot\sin \dfrac{\alpha }{2}\cdot\left( \cos \dfrac{\alpha }{2}-\dfrac{\sin \dfrac{\alpha }{2}}{\mathrm{tg}\alpha}\right)=$

$=R^2\left( 2\sin \dfrac{\alpha }{2}\cos \dfrac{\alpha }{2}-\dfrac{2\sin^2 \dfrac{\alpha }{2}}{\mathrm{tg}\alpha}\right)=R^2\left( \sin \alpha-\dfrac{2\cdot\dfrac{1-\cos\alpha }{2}} {\mathrm{tg}\alpha}\right)=$

$=R^2\left( \sin \alpha-\dfrac{1-\cos\alpha} {\mathrm{tg}\alpha}\right)=R^2\left( \sin \alpha-\dfrac{(1-\cos\alpha)\cos\alpha } {\sin\alpha}\right)=$

$=R^2\cdot \dfrac{\sin^2\alpha -(1-\cos\alpha)\cos\alpha } {\sin\alpha}=R^2\cdot\dfrac{\sin^2\alpha -\cos\alpha+\cos^2\alpha } {\sin\alpha}=$

$=R^2\cdot\dfrac{1 -\cos\alpha } {\sin\alpha}=R^2\cdot\mathrm{tg}\dfrac{\alpha }{2}$

Значит, наибольшая площадь прямоугольника равна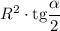 $R^2\cdot\mathrm{tg}\dfrac{\alpha }{2}$

ответ: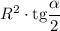 $R^2\cdot\mathrm{tg}\dfrac{\alpha }{2}$

В сектор AOB радиуса R с центральным углом 2α вписали прямоугольник наибольшей площади, симметричный

0,0(0 оценок)

Ответ:

saida1808

01.08.2020 00:28

Общая формула прямой: y=kx+b, где k - угол наклона к оси Ох, а b - смещение по у.

Найдем сначала k: k = тангенсу угла, образованного прямой и осью Ох. Образуем прямоуг. треугольник (как угодно), чтобы найти тангенс. Самый простой - "верхняя часть" показанной функции. Тангенс = 4 (катет = 4 поделить на катет = 1)

Если без тангенса, то можно вычислить логически: за ∆х = 1, ∆у = 4, k - это "скорость" возрастания функции, следует k = 4.

b найти еще проще, смещение по у = -4, следует b = -4.

Иначе, чтобы найти b, нужно чтобы формула приняла вид y = b, такое возможно при х =0. Находим на графике координаты у при х = 0, у = -4, следует b = -4.

Подставляем в формулу:

y = 4x - 4

0,0(0 оценок)

Популярные вопросы: Алгебра