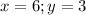Построим графики полученных уравнений: мы привели их к виду уравнения прямой
у = kx + b,
k - тангенс угла наклона прямой
b - смещение графика от (0,0) вдоль оси Оу
Построили. См рис.
(Пояснения: рядом с самими графиками написаны исходные уравнения, данные в условии. Внизу же, под сеткой координат - записаны функции вида у = kх + b. В принципе, это одно и то же)
Очевидно, решением системы будет точка пересечения графиков функций.
Данную систему уравнений можно решить банальным методом подстановки, из одного уравнения вычленяя переменную x или y и подставляя ее во второе уравнение.
Но есть и другие решения, я покажу как решить данную систему уравнений методом исключения переменных, что на мой взгляд, гораздо проще с данной системой.
Запишем систему уравнений:
Мы можем избавиться от переменной y. Для этого умножаем и правую, и левую части второго уравнения на 6:
Теперь исключаем переменную y путём сложения двух уравнений. Для начала прибавим второе уравнение системы к первому:
Так как сумма двух противоположных величин и равна нулю, удаляем их из нашего выражения:
Теперь мы легко получаем значение x из данного уравнения:
Теперь нам осталось подставить данное значение x во второе уравнение системы:
х = -2; у = 3
или
(-2; 3)
Объяснение:
Построим графики полученных уравнений: мы привели их к виду уравнения прямой
у = kx + b,
k - тангенс угла наклона прямой
b - смещение графика от (0,0) вдоль оси Оу
Построили. См рис.
(Пояснения: рядом с самими графиками написаны исходные уравнения, данные в условии. Внизу же, под сеткой координат - записаны функции вида у = kх + b. В принципе, это одно и то же)
Очевидно, решением системы будет точка пересечения графиков функций.
В нашем случае точка пересечения имеет координаты
х = -2; у = 3
или
(-2; 3)
Объяснение:
Данную систему уравнений можно решить банальным методом подстановки, из одного уравнения вычленяя переменную x или y и подставляя ее во второе уравнение.
Но есть и другие решения, я покажу как решить данную систему уравнений методом исключения переменных, что на мой взгляд, гораздо проще с данной системой.
Запишем систему уравнений:
Мы можем избавиться от переменной y. Для этого умножаем и правую, и левую части второго уравнения на 6:
Теперь исключаем переменную y путём сложения двух уравнений. Для начала прибавим второе уравнение системы к первому:
Так как сумма двух противоположных величин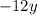
и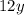 
равна нулю, удаляем их из нашего выражения:
Теперь мы легко получаем значение x из данного уравнения:
Теперь нам осталось подставить данное значение x во второе уравнение системы:
Находим y:
Получили ответ: