Жүрдек пойыз бағдаршам жанында 16 минут тұрып қалғандықтан, қалған 80км жолды ғын 10 км/сағ арттыра отырып уақытыңда жетті. пойыздың кесте бойыңша белгіленген ғын табыңдар​

1)

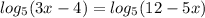
Область определения

{ 3x - 4 > 0; x > 4/3

{ 12 - 5x > 0; x < 12/5

D(x): x ∈ (4/3; 12/5)

Так как основания логарифмов одинаковые, то и выражения под логарифмами равны.

3x - 4 = 12 - 5x

3x + 5x = 12 + 4

8x = 16; x = 2 ∈ (4/3; 12/5) - это решение.

2)

Область определения:

x^2 + 3x - 7 > 0

D = 3^2 - 4*1(-7) = 9 + 28 = 37

x1 = (-3 - √37)/2 ≈ -4,541; x2 = (-3 + √37)/2 ≈ 1,541

D(x) : x ∈ (-oo; (-3-√37)/2) U ((-3+√37)/2; +oo)

Логарифм - это показатель степени, в которую надо возвести основание, чтобы получить число под логарифмом.

x^2 + 3x - 7 = 3^1 = 3

x^2 + 3x - 10 = 0

(x + 5)(x - 2) = 0

x1 = -5 ∈ D(x); x2 = 2 ∈ D(x) - это два решения.

3)

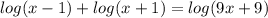
К сожалению, мы не знаем основание логарифма, но это неважно.

Главное, что основание должно быть везде одинаковое.

Область определения:

{ x > 1

{ x > -1

D(x) : x ∈ (1; +oo)

Решаем уравнение

Так как основание везде одинаковое, можно перейти к выражениям

(x - 1)(x + 1) = 9x + 9 = 9(x + 1)

Так как x = -1 не может быть, то делим все на (x + 1)

x - 1 = 9

x = 10 - это решение.

Формула нахождения координаты х вершины параболы 
а координату y будем находить методом подстановки x
а). так как b здесь равен нулю, то при делении нуля получаем 0
х верш = 0
у верш = 0
координата точки (0;0)
б). после подстановки в формулу и решения выражения получаем
х верш = 1,5
у верш = - 1,5
координата точки (1,5;-1,5)
в) то же самое, подставляем в формулу и получаем
х верш = -5
у верш = 5
координата точки (-5;5)
г). для удобства раскроем скобки, получим выражение: x^ - 2x +1
и по формуле:
х верш = 1
у верш = 0
координата точки (1;0)
д). опять раскроем скобки, получим 2(x^+6x+9) =  2x^ + 12x +18
х верш = -3
у верш = 0
координаты точки (-3;0)
е). x^ - 4x +3
х верш = 2
у верш = 1
координата точки (2;1)