знайдіть остачу від ділення многочлена
x3+3x2−2 на x+2.
а: 18
б: -6
в: 2
г: -22
д: -2
при якому значенні
a
многочлен
p(x)=−3x3+2x2+a ділиться без остачі на x−2?
а: -32
б: 16
в: 1
г: 32
д: -16
многочлен p(x) ділиться без остачі на x+1, а при діленні на x−2 дає остачу -3. знайдіть остачу від ділення многочлена
p(x) на x2−x−2.
а: −x−1
б: −x+1
в: 2
г: x−1
д: x+1
використовуючи теорему безу, знайдіть всі раціональні корені рівняння
2x3−3x2−11x+6=0
.а: −2; 1/2; 3
б: 12
в: 3
г: 2
д: −2
розкладіть на множники з цілими коефіцієнтами многочлен 2x3−5x2−x+6.
а: (x+1)(x−2)(x−32)
б: (x−1)(x−2)
в: (x+1)(x−2)(x−3)
г: 2(x+1)(x−2)(x−32)
д: 2(x−1)(x−2)(x+32)
1) Пусть х км/ч — скорость второго автомобиля ( х > 0).
2) Тогда (х + 10) км/ч — скорость первого.
3) (300 : (х + 10)) ч. — столько времени уходит у первого автомобиля на преодоление пути в 300 км.
4) (300 : х) ч. — за столько времени второй автомобиль проезжает те же 300 км.
5) По условию задачи первый автомобиль тратит на данный путь на 1 час меньше, чем второй, поэтому записываем равенство:
300 : х - 300 : (х + 10) = 1.
6) Решаем уравнение:
300 * (х + 10) - 300 * х = х * (х + 10);
300х + 3000 - 300х = х^2 + 10х;
х^2 + 10х - 3000 = 0.
По теореме Виета находим, что х1 = -60, х2 = 50.
7) Так как -60 < 0, то х1 не является решением задачи.
8) Значит, х = 50 км/ч — скорость второго автомобиля.
9) Узнаем скорость первого:
50 + 10 = 60 км/ч.
ответ: 60 и 50 км/ч.
Объяснение:
вот так примерно
№1) 1)0.25x>1 2)1-6x>=0 3)5y-7-6< 4y-1.5
x>1/0.25 6x=<1 y<11.5
x>4 x<=1/6
№2)
m+1<3m-18
-2m< -19
m> 9.5
№3
А)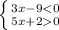 Б)
Б) 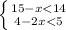
ответ: x принадлежит {-0.4 ; 3} ответ: X больше 1
№4
Б)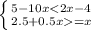
1; 2; 3; 4; 5
ОДЗ