1. Здесь мы учитываем порядок, значит используем размещение. Первым моджет быть один из пяти предметов, вторым, один из четырех и т.д.120
2. Здесь необходимо использовать сочетание, а не размещение, так как нам необходимо считать наборы отличающиеся только порядком элементов - одинаковыми (например: {1,2,3,4},{1,3,2,4}) . Сочетание же различает только те наборы у которых различается состав элементов.
= 35960
3. На первую позицию можно поставить одно из шести чисел, на вторую, одно из оставшихся пяти: 6*5 = 30
12 21 31 41 51 61
13 23 32 42 52 62
14 24 34 43 53 63
15 25 35 45 54 64
16 26 36 46 56 65
4. n = 45, w = 17, b = 45 - 17 = 28
После того, как потеряли два не белых шарика, осталось n = 43, w = 17, b = 26
Вероятность вытащить белый равна 17/43 (количество положительных исходов, ко всем исходам)
5. Всего возможных исходов(1 - орел, 0 - решка):
000
001
010
011
100
101
110
111
n = 8. ()
Положительных исходов: 011, 101, 110. m = 3 ()
p = 3/8
Если же нам необходимо выпадение именно набора 110 (орел орел решка), тогда положительный исход один и вероятность будет 1/8
6. Всего исходов n = 1000000, положительных m = 1200+800 = 2000, p(m) = 2000/1000000 = 2/1000 = 0.002
7. Двухзначных чисел всего 90. Первое двузначное число 10, последнее 99. При делении на 13 даёт в остатке 5, число 18. Следующее 18+13 = 31, потом 44, 57, 70, 83, 96. Таких чисел 7.
Вероятность выбрать двухзначное число, которое будет давать остаток 5 при делении на 13 = 7/90 (число положительных исходов к числу всех исходов)
Число составления расписания равно числу перестановок из пяти.
2. Число выбрать четырёх человек для участия в математической олимпиаде равно числу сочетания из 32 по 4(порядок выбора учеников не важен) :
3. На первое место можно выбрать любые из шести заданных цифр, то есть, можно выбрать на второе месте можно выбрать оставшиеся из пяти цифр
По правилу произведения, составить различных двузначных чисел можно
4. Всего шариков изначально было 45+17= 62 и два шарика потеряли(белых), тогда останется всего 60 шариков из них 15 белых.
Вероятность того, что выбранный наугад шарик будет белым равна
P=15/60 = 0.25
5. Всего все возможных подбрасывания трёх монет равно 2³ = 8 из них перечислим благоприятные.
Искомая вероятность: P = 3/8 = 0.375
6. Всего все возможных выбора билетов - 1000000 среди них 1200+800 = 2000 выигрышных.
Искомая вероятность: P=2000/1000000=0.002
7. Всего двузначных чисел 99-9=90 из них есть те числа которые при делении на 13 даёт в остатке 5:
18; 31; 44; 57; 70; 83; 96 - всего 7
Искомая вероятность: P = 7/90.
1. Здесь мы учитываем порядок, значит используем размещение. Первым моджет быть один из пяти предметов, вторым, один из четырех и т.д.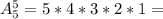 120
120
2. Здесь необходимо использовать сочетание, а не размещение, так как нам необходимо считать наборы отличающиеся только порядком элементов - одинаковыми (например: {1,2,3,4},{1,3,2,4}) . Сочетание же различает только те наборы у которых различается состав элементов.
3. На первую позицию можно поставить одно из шести чисел, на вторую, одно из оставшихся пяти: 6*5 = 30
12 21 31 41 51 61
13 23 32 42 52 62
14 24 34 43 53 63
15 25 35 45 54 64
16 26 36 46 56 65
4. n = 45, w = 17, b = 45 - 17 = 28
После того, как потеряли два не белых шарика, осталось n = 43, w = 17, b = 26
Вероятность вытащить белый равна 17/43 (количество положительных исходов, ко всем исходам)
5. Всего возможных исходов(1 - орел, 0 - решка):
000
001
010
011
100
101
110
111
n = 8. (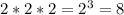 )
)
Положительных исходов: 011, 101, 110. m = 3 (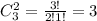 )
)
p = 3/8
Если же нам необходимо выпадение именно набора 110 (орел орел решка), тогда положительный исход один и вероятность будет 1/8
6. Всего исходов n = 1000000, положительных m = 1200+800 = 2000, p(m) = 2000/1000000 = 2/1000 = 0.002
7. Двухзначных чисел всего 90. Первое двузначное число 10, последнее 99. При делении на 13 даёт в остатке 5, число 18. Следующее 18+13 = 31, потом 44, 57, 70, 83, 96. Таких чисел 7.
Вероятность выбрать двухзначное число, которое будет давать остаток 5 при делении на 13 = 7/90 (число положительных исходов к числу всех исходов)