ответ:10 часов 15 минут
Ну для начала смотрим, что отец и сын встретились на расстоянии 12 км от Кальтухи, отец же выехал из Кальтухи, значит отец проехал 12 км
А сын проехал:1) 30,75км - 12км = 18,75 км
2)узнаем сколько часов ехал Эмиль для этого расстояние делим на скорость: 18,75 : 15км/ч = 1(ч) 15(м)
3)10ч + 1ч 15м= 11(ч) 15(м)- это во столько они встретились
4)Узнаем сколько по времени ехал отец: 12км : 12км/ч = 1(ч)
5)А теперь, на сколько позже выехал отец: 1ч 15 м - 1ч = 15м
6)10ч(во столько выехал Эмиль)+ 15 минут(на столько позже выехал отец)=10ч 15 м: в это время выехал отец из Кальтухи.
Вроде бы так) Удачи
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если , а , при k>5
То есть, , при k>5, то по закону транзитивности:
, при k>5 - ч.т.д
ответ:10 часов 15 минут
Ну для начала смотрим, что отец и сын встретились на расстоянии 12 км от Кальтухи, отец же выехал из Кальтухи, значит отец проехал 12 км
А сын проехал:1) 30,75км - 12км = 18,75 км
2)узнаем сколько часов ехал Эмиль для этого расстояние делим на скорость: 18,75 : 15км/ч = 1(ч) 15(м)
3)10ч + 1ч 15м= 11(ч) 15(м)- это во столько они встретились
4)Узнаем сколько по времени ехал отец: 12км : 12км/ч = 1(ч)
5)А теперь, на сколько позже выехал отец: 1ч 15 м - 1ч = 15м
6)10ч(во столько выехал Эмиль)+ 15 минут(на столько позже выехал отец)=10ч 15 м: в это время выехал отец из Кальтухи.
Вроде бы так) Удачи
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если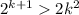
, а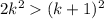 
, при k>5
То есть,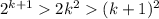
, при k>5, то по закону транзитивности: