Знайти значення похідної в точці

Объяснение:

Нам даны несколько уравнений вида

P(t)=at²+bt+c. Т.е. многочлен второй степени от какой-нибудь переменной,t,x,m,n в принципе любые)

Дискриминант считается как

а корни квадратного многочлена находятся по формуле

если D>0, то у нас 2 различных корня, если D=0, то у нас 2 совпадающих корня x1=x2, если же D<0, то корней на мн-ве действительных чисел нет, т.к. корни из отрицательных чисел мы пока извлекать не научились. А теперь пользуемся формулой

1)D=2²-4*1*(-24)=4+96=100(√D=10>0)

x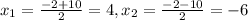

3)D=(-9)²-4*10*2=81-80=1(√D=1>0)

8)D=100-148=-48<0, следовательно корней у уравнения нет.

3) заметим, что (4х-1)(4х+1)=16x²-1, а (3х-5)²=9x²-30x+25, тогда

9x²+16x²-30x+25-1-29=0

25x²-30x-5=0 разделим уравнение на 5,

5x²-6x-1=0

D=36+20=56(√D=2√14>0)

последнее я уже говорил, что один корень уравнение имеет, когда дискриминант равен 0

D=m²-4*12*3=m²-12²=(m-12)(m+12)

D=0⇔(m-12)(m+12)=0⇔m=±12

1) квадратное уравнение с модулем будет иметь не менее трех корней если прямая а проходит через вершину параболы -(x^2-6x-5) - это верхнее значение параметра,

а нижнее а=0.

находим вершину параболы, х0=-b/2a у нам b=6 a=-1  x0=3

y0=-9+5+18=14

значит а [0;14]

2) sqrt(x-1)=a+x  x>=1

x-1=x^2+a^2+2ax

x^2+(2a-1)x+a^2+1=0

D>0  (2a-1)^2-4a^2-4>0  -4a-3>0  a<-3/4

3) 4x^2-15x+4a^3=0

x1=x2^2

x1*x2=a^3

x2^3=a^3  x2=a

15/4=x1+x2  15/4=a^2+a

4a^2+4a-15=0  a1=3/2  a2=-5/2

x^2-ax+(a-1)=0

x1^2+x2^2=(x1+x2)^2-2x1x2=17

a^2-2(a-1)=17

a^2-2a-15=0

a1=5 a2=-3