Алфавит внутренних состояний Q = {, } — рабочее состояние и остановка соответственно.
Начальное положение — над первым символом слова.
Будем последовательно считывать символы на ленте, двигаясь по ней слева направо. Если считали 1, просто переходим в соседнюю ячейку:
(R (right) — то же самое, что и П на скриншоте)
Если считали пустой символ , то мы попали в ячейку сразу после ячейки с последним символом заданного слова. Заменяем этот пустой символ на единицу и останавливаемся:
Построили машину Тьюринга, которая слово вида преобразовывает в слово вида
12.17
Внешний алфавит A = {, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0} — пустой символ и все цифры десятичной системы счисления.
Алфавит внутренних состояний Q = {, } — рабочее состояние и остановка соответственно.
Функциональная схема (программа):
(для i = 1, 2,..., 9)
(L (left) — то же самое, что и Л на скриншоте)
(для i = 1, 2,..., 9)
Начальное положение — над последним символом слова на входе (как написано в тексте на скриншоте, стандартное положение).
Пояснение к работе построенной машины. Если отнимание единицы из последней цифры не требует перехода 10-ти из разряда слева, то просто вычитаем и останавливаемся (первая команда). Но если последняя цифра — ноль, то после замены его на 9 придется перейти к символу слева (вторая команда) и с ним повторить все те же действия, что и с последним символом. И так до тех пор, пока не встретим символ, отнимание единицы из которого не требует перехода 10-ти из разряда слева. Короче говоря, все как при обычном вычитании в столбик. Последние три команды убирают (заменяют на пустые символы) ведущие нули, если они, конечно, появились.
пошв результате развития человеческого общества появилась необходимость в измерении длины, площади, веса и т. д. в этом деле не обойтись одними целыми числами, люди ввели дроби.
вначале это были так называемые «обыкновенные дроби». главное их неудобство состояло в том, что долями единицы (знаменателями) могли быть любые числа. и в процессе счета нужно было приводить дроби к одному знаменателю. тогда появилась идея создания систематических дробей, в которых единица всегда имеет одинаковое число долей.
самые первые систематические дроби появились в вавилоне за 2 тысячи лет до нашей эры. в них единица делилась на шестьдесят долей, так как «круглым» числом у вавилонян считалось не 10, а 60. вавилонские дроби, в отличие от всей шестидесятеричной системы счета, были заимствованы древними греками, а от них и европейцами. этой системой пользовались в западной европе, в основном астрономы, до конца xvi века.
в древнем риме существовала двенадцатеричная система дробей (единица делилась на двенадцать долей). это было связано с тем, что денежная единица древних римлян (она же единица веса) асc делилась на двенадцать унций. унцией называли не только мелкую монету, но и вообще дробь, которую мы называем «одна двенадцатая», даже если она употреблялась для измерения длины.
наши обыкновенные дроби широко употреблялись древними греками и индийцами. правила действий с дробями, изложенные индийским ученым брамагуптой, в ix веке распространились в мусульманских странах мухаммеду хорезмскому. в западную европу их итальянский купец и ученый леонардо фибоначчи из пизы в xiii веке.
наконец, самаркандский гиясэддин джемшид ал-каши (xiv-xv века) ввел десятичные дроби, которыми мы пользуемся и сейчас. когда в xvi веке голландский купец и инженер симон стевин познакомил с ними европу, они полностью вытеснили громоздкие шестидесятеричные дроби.
12.14
Функциональная схема (программа):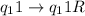
, 
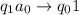
12.17
смотри объяснение
Объяснение:
12.14
Алфавит внутренних состояний Q = {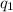
, 
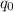} — рабочее состояние и остановка соответственно.
Начальное положение — над первым символом слова.
Будем последовательно считывать символы на ленте, двигаясь по ней слева направо. Если считали 1, просто переходим в соседнюю ячейку:
Если считали пустой символ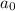
, то мы попали в ячейку сразу после ячейки с последним символом заданного слова. Заменяем этот пустой символ на единицу и останавливаемся:
Построили машину Тьюринга, которая слово вида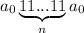
преобразовывает в слово вида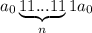 
12.17
Внешний алфавит A = {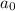
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0} — пустой символ и все цифры десятичной системы счисления.
Алфавит внутренних состояний Q = {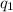
, 
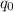} — рабочее состояние и остановка соответственно.
Функциональная схема (программа):
Начальное положение — над последним символом слова на входе (как написано в тексте на скриншоте, стандартное положение).
Пояснение к работе построенной машины. Если отнимание единицы из последней цифры не требует перехода 10-ти из разряда слева, то просто вычитаем и останавливаемся (первая команда). Но если последняя цифра — ноль, то после замены его на 9 придется перейти к символу слева (вторая команда) и с ним повторить все те же действия, что и с последним символом. И так до тех пор, пока не встретим символ, отнимание единицы из которого не требует перехода 10-ти из разряда слева. Короче говоря, все как при обычном вычитании в столбик. Последние три команды убирают (заменяют на пустые символы) ведущие нули, если они, конечно, появились.
ответ:
пошв результате развития человеческого общества появилась необходимость в измерении длины, площади, веса и т. д. в этом деле не обойтись одними целыми числами, люди ввели дроби.
вначале это были так называемые «обыкновенные дроби». главное их неудобство состояло в том, что долями единицы (знаменателями) могли быть любые числа. и в процессе счета нужно было приводить дроби к одному знаменателю. тогда появилась идея создания систематических дробей, в которых единица всегда имеет одинаковое число долей.
самые первые систематические дроби появились в вавилоне за 2 тысячи лет до нашей эры. в них единица делилась на шестьдесят долей, так как «круглым» числом у вавилонян считалось не 10, а 60. вавилонские дроби, в отличие от всей шестидесятеричной системы счета, были заимствованы древними греками, а от них и европейцами. этой системой пользовались в западной европе, в основном астрономы, до конца xvi века.
в древнем риме существовала двенадцатеричная система дробей (единица делилась на двенадцать долей). это было связано с тем, что денежная единица древних римлян (она же единица веса) асc делилась на двенадцать унций. унцией называли не только мелкую монету, но и вообще дробь, которую мы называем «одна двенадцатая», даже если она употреблялась для измерения длины.
наши обыкновенные дроби широко употреблялись древними греками и индийцами. правила действий с дробями, изложенные индийским ученым брамагуптой, в ix веке распространились в мусульманских странах мухаммеду хорезмскому. в западную европу их итальянский купец и ученый леонардо фибоначчи из пизы в xiii веке.
наконец, самаркандский гиясэддин джемшид ал-каши (xiv-xv века) ввел десятичные дроби, которыми мы пользуемся и сейчас. когда в xvi веке голландский купец и инженер симон стевин познакомил с ними европу, они полностью вытеснили громоздкие шестидесятеричные дроби.
аговое объяснение: