1. Струя жидкости со скоростью V бьет в неподвижную стену перпендикулярно ее поверхности. Найдите давление, которое производит жидкость на стену в точке, находящейся на оси струи. Атмосферное давление Po, плотность жидкости p.

1.Период обращения ИСЗ составляет 1 ч 40 мин 47 с. На какой высоте над поверхностью Земли движется спутник? Радиус Земли R = 6400 км, масса Земли М = 6 • 1024 кг.

Дано

Т=1 ч 40 мин 47 с =6047 с

R = 6400 км= 6400000 м=6.4*10^6 м

масса Земли М = 6*10^24 кг

G= 6,6725×10-11 м³/(кг·с²). гравитационная постоянная

H -?

РЕШЕНИЕ

F=GmM/(R+H)^2

ma=GmM/(R+H)^2

a=GM/(R+H)^2

v^2/R=GM/(R+H)^2

(2pi/T)^2*R=GM/(R+H)^2

(2pi/T)^2*R/GM=1/(R+H)^2

GM/((2pi/T)^2*R)=(R+H)^2

√(GM/((2pi/T)^2*R))=R+H

H=√(GM/((2pi/T)^2*R))-R

H=√(6.6725*10^-11*6*10^24/((2pi/6047)^2*6.4*10^6)) - 6.4*10^6=1.21185*10^6 м

  =1211.85*10^3 км

ответ 1.21185*10^6 м  =1211.85*10^3 км

Движение равноускоренное, путь вычисляется по формуле:

, так как начальная скорость равна нулю

Из этой формулы узнаем время падения тела:

, где g=9,8 - ускорение свободного падения

Подставляя числа в формулу, находим:

6 секунд пролетело тело до столкновения с землёй. Для того, чтобы узнать, сколько оно пролетело за предпоследнюю секунду, надо узнать, какую скорость оно имело после 4-х секунд времени(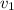), и какую скорость оно имело после 5-ти секунд времени().

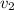Так как начальная скорость равна нулю,

м/с

м/с

Теперь найдем пройденный за предпоследнюю секунду путь по формуле:

м

Узнаем путь, пройденный за последнюю секунду, для этого найдем скорость тела в момент столкновения с землей:

м/с

Тогда

м

ответ: за предпоследнюю перед приземлением секунду тело м, а за последнюю - 53,9м.