4. Із замкнутої дротяної котушки виймають постійний магніт, як показано рисунку. Визначте напрямок індукційного струму в котушці. Свою відповідь обґрунтуйте. ( ) на й
Период вращения — время одного полного оборота. Период вращения {\displaystyle T}T и его частота {\displaystyle \nu }\nu связаны соотношением {\displaystyle T=1/\nu }{\displaystyle T=1/\nu }.
Линейная скорость точки, находящейся на расстоянии {\displaystyle R}R от оси вращения
{\displaystyle v={2\pi \nu R}={2\pi R \over T},}{\displaystyle v={2\pi \nu R}={2\pi R \over T},}
Угловая скорость вращения тела — аксиальный вектор (псевдовектор).
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:
В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы
Момент инерции — физическая величина, мера инертности тела во вращательном движении. Характеризует распределение масс в теле. Различают осевой и центробежный момент инерции. Осевой момент инерции определяется равенством:
Нужно, чтобы фокусы обеих линз справа от них были совмещены, тогда требование задачи выполнится. Фокусы могут быть разными по модулю. В случае, когда они равны по модулю, то линзы надо ставить плотно, как и было указано в таком частном случае.
Объяснение:
Краткое объяснение на втором изображении.
Далее – полное объяснение.
Поставим на одной оптической оси положительную линзу с фокусным расстоянием и соответствующей силой и отрицательную линзу с фокусным расстоянием и соответствующей силой , как показано на чертеже.
Направим тонкий пучок света на поверхность положительной линзы под углом к главной оптической оси в точку , отстоящую от оптической оси на расстояние .
Проведём воображаемый луч через главный оптический центр положительной линзы параллельно пучку света до пересечения с фокальной плоскостью положительной линзы в точке . По правилам построения изображения в тонких линзах, в точку направится и пучок света сразу после преломления положительной линзой. Отсюда мы можем найти угол , преломления пучка света в положительной линзе:
;
Понятно, что под тем же углом к главной оптической оси первично преломленный в положительной линзе пучок упадёт на поверхность отрицательной линзы.
Пусть линзы установлены на расстоянии друг от друга, тогда, как легко найти по чертежу, точка падения пучка на поверхность отрицательной линзы, отстоит от оптической оси на расстояние:
.
Будем считать, что данный пучок между линзами направлен в некоторую точку фокальной плоскости отрицательной линзы. После вторичного преломления в отрицательной линзе пучок отклонится от этой точки вверх.
Проведём воображаемый луч через главный оптический центр отрицательной линзы. По правилам построения изображения в тонких линзах, пучок света сразу после преломления отрицательной линзой, направится параллельно построенному воображаемому лучу. Отсюда мы можем найти угол , полного преломления пучка по прохождении света через обе линзы:
;
Отсюда хорошо видно, что если мы направим широкий параллельный пучок на положительную линзу под некоторым углом к главной оптической оси, с разными по ширине пучка значениями вертикальной координаты точки падения , то угол преломления по прохождении через обе линзы окажется независимым от координаты лишь в том случае, когда выполняется условие:
, где .
Т.е., короче говоря, правые фокусы положительной и отрицательной линзы должны быть точно совмещены, тогда любые параллельные лучи слева после преломления окажутся параллельными и справа.
Вообще, это рассуждение так же верно и для случая:
, где и , только в этом случае нужно совместить фокусы положительных линз, находящиеся между ними.
В обоих случаях мы получим телескоп или микроскоп! В случае с положительными линзами – классическую схему, а в случае с правой отрицательной – схему Ньютона.
, в котором увеличение объектов и увеличение угла преломления параллельного пучка – суть две стороны одной медали:
Объяснение:
Кинематические характеристики
Вращение характеризуется углом измеряющимся в градусах или радианах, угловой скоростью {\displaystyle \omega ={\frac {d\varphi }{dt}}}\omega ={\frac {d\varphi }{dt}} (измеряется в рад/с) и угловым ускорением {\displaystyle \epsilon ={\frac {d^{2}\varphi }{dt^{2\epsilon ={\frac {d^{{2}}\varphi }{dt^{{2 (единица измерения — рад/с²).
При равномерном вращении ({\displaystyle T}T — период вращения),
Частота вращения — число оборотов в единицу времени.
{\displaystyle \nu ={1 \over T}={\omega \over 2\pi },}{\displaystyle \nu ={1 \over T}={\omega \over 2\pi },}
Период вращения — время одного полного оборота. Период вращения {\displaystyle T}T и его частота {\displaystyle \nu }\nu связаны соотношением {\displaystyle T=1/\nu }{\displaystyle T=1/\nu }.
Линейная скорость точки, находящейся на расстоянии {\displaystyle R}R от оси вращения
{\displaystyle v={2\pi \nu R}={2\pi R \over T},}{\displaystyle v={2\pi \nu R}={2\pi R \over T},}
Угловая скорость вращения тела — аксиальный вектор (псевдовектор).
{\displaystyle \omega ={2\pi \nu }={2\pi \over T}.}{\displaystyle \omega ={2\pi \nu }={2\pi \over T}.}
Динамические характеристики
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:
{\displaystyle E={\frac {\omega ^{2}J}{2}}={2\pi ^{2}\nu ^{2}J}.}{\displaystyle E={\frac {\omega ^{2}J}{2}}={2\pi ^{2}\nu ^{2}J}.}
В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы
{\displaystyle J=\int r^{2}dm.}{\displaystyle J=\int r^{2}dm.}
Момент инерции — физическая величина, мера инертности тела во вращательном движении. Характеризует распределение масс в теле. Различают осевой и центробежный момент инерции. Осевой момент инерции определяется равенством:
{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}
где {\displaystyle m_{i}}m_i — масса, {\displaystyle r_{i}}r_{i} — расстояние от {\displaystyle i}i-й точки до оси
Нужно, чтобы фокусы обеих линз справа от них были совмещены, тогда требование задачи выполнится. Фокусы могут быть разными по модулю. В случае, когда они равны по модулю, то линзы надо ставить плотно, как и было указано в таком частном случае.
Объяснение:
Краткое объяснение на втором изображении.
Далее – полное объяснение.
Поставим на одной оптической оси положительную линзу с фокусным расстоянием и соответствующей силой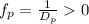 и отрицательную линзу с фокусным расстоянием и соответствующей силой
и отрицательную линзу с фокусным расстоянием и соответствующей силой 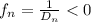 , как показано на чертеже.
, как показано на чертеже.
Направим тонкий пучок света на поверхность положительной линзы под углом к главной оптической оси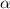 в точку
в точку 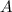 , отстоящую от оптической оси на расстояние
, отстоящую от оптической оси на расстояние 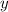 .
.
Проведём воображаемый луч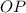 через главный оптический центр положительной линзы параллельно пучку света до пересечения с фокальной плоскостью положительной линзы в точке
через главный оптический центр положительной линзы параллельно пучку света до пересечения с фокальной плоскостью положительной линзы в точке 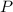 . По правилам построения изображения в тонких линзах, в точку
. По правилам построения изображения в тонких линзах, в точку 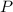 направится и пучок света сразу после преломления положительной линзой. Отсюда мы можем найти угол
направится и пучок света сразу после преломления положительной линзой. Отсюда мы можем найти угол 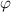 , преломления пучка света в положительной линзе:
, преломления пучка света в положительной линзе:
Понятно, что под тем же углом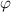 к главной оптической оси первично преломленный в положительной линзе пучок упадёт на поверхность отрицательной линзы.
к главной оптической оси первично преломленный в положительной линзе пучок упадёт на поверхность отрицательной линзы.
Пусть линзы установлены на расстоянии друг от друга, тогда, как легко найти по чертежу, точка
друг от друга, тогда, как легко найти по чертежу, точка 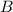 падения пучка на поверхность отрицательной линзы, отстоит от оптической оси на расстояние:
падения пучка на поверхность отрицательной линзы, отстоит от оптической оси на расстояние:
Будем считать, что данный пучок между линзами направлен в некоторую точку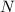 фокальной плоскости отрицательной линзы. После вторичного преломления в отрицательной линзе пучок отклонится от этой точки вверх.
фокальной плоскости отрицательной линзы. После вторичного преломления в отрицательной линзе пучок отклонится от этой точки вверх.
Проведём воображаемый луч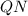 через главный оптический центр отрицательной линзы. По правилам построения изображения в тонких линзах, пучок света сразу после преломления отрицательной линзой, направится параллельно построенному воображаемому лучу. Отсюда мы можем найти угол
через главный оптический центр отрицательной линзы. По правилам построения изображения в тонких линзах, пучок света сразу после преломления отрицательной линзой, направится параллельно построенному воображаемому лучу. Отсюда мы можем найти угол 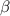 , полного преломления пучка по прохождении света через обе линзы:
, полного преломления пучка по прохождении света через обе линзы:
Отсюда хорошо видно, что если мы направим широкий параллельный пучок на положительную линзу под некоторым углом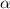 к главной оптической оси, с разными по ширине пучка значениями вертикальной координаты точки падения
к главной оптической оси, с разными по ширине пучка значениями вертикальной координаты точки падения 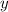 , то угол преломления по прохождении через обе линзы окажется независимым от координаты
, то угол преломления по прохождении через обе линзы окажется независимым от координаты 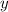 лишь в том случае, когда выполняется условие:
лишь в том случае, когда выполняется условие:
Т.е., короче говоря, правые фокусы положительной и отрицательной линзы должны быть точно совмещены, тогда любые параллельные лучи слева после преломления окажутся параллельными и справа.
Вообще, это рассуждение так же верно и для случая:
В обоих случаях мы получим телескоп или микроскоп! В случае с положительными линзами – классическую схему, а в случае с правой отрицательной – схему Ньютона.