W = Iω2/2 (энергия равна моменту инерции вращающейся системы помноженного на половину квадрата угловой скорости)
Когда человек сближает гири, у него, на самом деле, сгибаются ещё и руки в локтях. Поэтому момент инерции человека тоже меняется, но этим можно пренебречь.
W1 = I1 общ.ω12/2 // Кинетическая энергия вращения до сближения гирь.
W2 = I2 общ.ω22/2 // Кинетическая энергия вращения после сближения гирь.
I1 общ. = 2I1 + Iчеловека // I1 - момент инерции одной гири до сближенния.
I2 общ. = 2I2 + Iчеловека // I1 - момент инерции одной гири после сближенния.
И что теперь?! Мы знаем всё, кроме момента инерции человека. Как же быть?! А очень просто. В описанном действии сохраняется момент количества движения. Слыхали о таком? Так вот в соответсвии с законом о сохранении момента количесва движения можно записать:
I1&omega1 = I2&omega2 // Здесь слева и справа стоят выражения называемые моментом количества движения (или момент импульса, т.к. это одно и тоже: кол-во движения ~ импульс)
2π(2I1 + Iчеловека)&nu1 = 2π(2I2 + Iчеловека)&nu2
Iчеловека(&nu2-&nu1) = 2I1ν1 - 2I2ν2
Iчеловека = (2I1ν1 - 2I2ν2)/(&nu2-&nu1)
Начнём численные рассчёты.
Можно было бы посчитать в общем виде, но мы не на экзамене.
I1 = mr12 = md12/4 = 2·1.52/4 = 1.125 кг·м2
I2 = mr22 = md22/4 = 2·0.82/4 = 0.32 кг·м2
Iчеловека = (2·1.125·1 - 2·0.32·1.5)/(1.5 - 1) = 2.58 кг·м2 (Я сейчас подумал и решил сообщить о поправке. Это не момент инерции человека, а момент инерции всей вращающейся системы исключая гири, т.е. человека, скамейки, содержимого карманов и т.п.)
Нужно, чтобы фокусы обеих линз справа от них были совмещены, тогда требование задачи выполнится. Фокусы могут быть разными по модулю. В случае, когда они равны по модулю, то линзы надо ставить плотно, как и было указано в таком частном случае.
Объяснение:
Краткое объяснение на втором изображении.
Далее – полное объяснение.
Поставим на одной оптической оси положительную линзу с фокусным расстоянием и соответствующей силой и отрицательную линзу с фокусным расстоянием и соответствующей силой , как показано на чертеже.
Направим тонкий пучок света на поверхность положительной линзы под углом к главной оптической оси в точку , отстоящую от оптической оси на расстояние .
Проведём воображаемый луч через главный оптический центр положительной линзы параллельно пучку света до пересечения с фокальной плоскостью положительной линзы в точке . По правилам построения изображения в тонких линзах, в точку направится и пучок света сразу после преломления положительной линзой. Отсюда мы можем найти угол , преломления пучка света в положительной линзе:
;
Понятно, что под тем же углом к главной оптической оси первично преломленный в положительной линзе пучок упадёт на поверхность отрицательной линзы.
Пусть линзы установлены на расстоянии друг от друга, тогда, как легко найти по чертежу, точка падения пучка на поверхность отрицательной линзы, отстоит от оптической оси на расстояние:
.
Будем считать, что данный пучок между линзами направлен в некоторую точку фокальной плоскости отрицательной линзы. После вторичного преломления в отрицательной линзе пучок отклонится от этой точки вверх.
Проведём воображаемый луч через главный оптический центр отрицательной линзы. По правилам построения изображения в тонких линзах, пучок света сразу после преломления отрицательной линзой, направится параллельно построенному воображаемому лучу. Отсюда мы можем найти угол , полного преломления пучка по прохождении света через обе линзы:
;
Отсюда хорошо видно, что если мы направим широкий параллельный пучок на положительную линзу под некоторым углом к главной оптической оси, с разными по ширине пучка значениями вертикальной координаты точки падения , то угол преломления по прохождении через обе линзы окажется независимым от координаты лишь в том случае, когда выполняется условие:
, где .
Т.е., короче говоря, правые фокусы положительной и отрицательной линзы должны быть точно совмещены, тогда любые параллельные лучи слева после преломления окажутся параллельными и справа.
Вообще, это рассуждение так же верно и для случая:
, где и , только в этом случае нужно совместить фокусы положительных линз, находящиеся между ними.
В обоих случаях мы получим телескоп или микроскоп! В случае с положительными линзами – классическую схему, а в случае с правой отрицательной – схему Ньютона.
, в котором увеличение объектов и увеличение угла преломления параллельного пучка – суть две стороны одной медали:
Объяснение:
W = Iω2/2 (энергия равна моменту инерции вращающейся системы помноженного на половину квадрата угловой скорости)
Когда человек сближает гири, у него, на самом деле, сгибаются ещё и руки в локтях. Поэтому момент инерции человека тоже меняется, но этим можно пренебречь.
W1 = I1 общ.ω12/2 // Кинетическая энергия вращения до сближения гирь.
W2 = I2 общ.ω22/2 // Кинетическая энергия вращения после сближения гирь.
I1 общ. = 2I1 + Iчеловека // I1 - момент инерции одной гири до сближенния.
I2 общ. = 2I2 + Iчеловека // I1 - момент инерции одной гири после сближенния.
ω1 = 2πν1
ω2 = 2πν2
ΔW = W2 - W1 = I2 общ.ω22/2 - I1 общ.ω12/2 = (2I2 + Iчеловека)2π2ν22 - (2I1 + Iчеловека)2π2ν12
И что теперь?! Мы знаем всё, кроме момента инерции человека. Как же быть?! А очень просто. В описанном действии сохраняется момент количества движения. Слыхали о таком? Так вот в соответсвии с законом о сохранении момента количесва движения можно записать:
I1&omega1 = I2&omega2 // Здесь слева и справа стоят выражения называемые моментом количества движения (или момент импульса, т.к. это одно и тоже: кол-во движения ~ импульс)
2π(2I1 + Iчеловека)&nu1 = 2π(2I2 + Iчеловека)&nu2
Iчеловека(&nu2-&nu1) = 2I1ν1 - 2I2ν2
Iчеловека = (2I1ν1 - 2I2ν2)/(&nu2-&nu1)
Начнём численные рассчёты.
Можно было бы посчитать в общем виде, но мы не на экзамене.
I1 = mr12 = md12/4 = 2·1.52/4 = 1.125 кг·м2
I2 = mr22 = md22/4 = 2·0.82/4 = 0.32 кг·м2
Iчеловека = (2·1.125·1 - 2·0.32·1.5)/(1.5 - 1) = 2.58 кг·м2 (Я сейчас подумал и решил сообщить о поправке. Это не момент инерции человека, а момент инерции всей вращающейся системы исключая гири, т.е. человека, скамейки, содержимого карманов и т.п.)
Досчитываем до конца.
ΔW = 2π2(ν22(Iчеловека + 2I2) - ν12(Iчеловека + 2I1)) = 2·3,142·(1.52(2.58 + 2·1.125) - 1·(2.58 + 2·0.32)) = 150.8 Дж.
ответ: На 150.8 джоулей.
Нужно, чтобы фокусы обеих линз справа от них были совмещены, тогда требование задачи выполнится. Фокусы могут быть разными по модулю. В случае, когда они равны по модулю, то линзы надо ставить плотно, как и было указано в таком частном случае.
Объяснение:
Краткое объяснение на втором изображении.
Далее – полное объяснение.
Поставим на одной оптической оси положительную линзу с фокусным расстоянием и соответствующей силой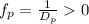 и отрицательную линзу с фокусным расстоянием и соответствующей силой
и отрицательную линзу с фокусным расстоянием и соответствующей силой 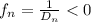 , как показано на чертеже.
, как показано на чертеже.
Направим тонкий пучок света на поверхность положительной линзы под углом к главной оптической оси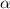 в точку
в точку 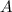 , отстоящую от оптической оси на расстояние
, отстоящую от оптической оси на расстояние 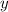 .
.
Проведём воображаемый луч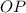 через главный оптический центр положительной линзы параллельно пучку света до пересечения с фокальной плоскостью положительной линзы в точке
через главный оптический центр положительной линзы параллельно пучку света до пересечения с фокальной плоскостью положительной линзы в точке 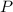 . По правилам построения изображения в тонких линзах, в точку
. По правилам построения изображения в тонких линзах, в точку 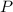 направится и пучок света сразу после преломления положительной линзой. Отсюда мы можем найти угол
направится и пучок света сразу после преломления положительной линзой. Отсюда мы можем найти угол 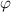 , преломления пучка света в положительной линзе:
, преломления пучка света в положительной линзе:
Понятно, что под тем же углом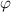 к главной оптической оси первично преломленный в положительной линзе пучок упадёт на поверхность отрицательной линзы.
к главной оптической оси первично преломленный в положительной линзе пучок упадёт на поверхность отрицательной линзы.
Пусть линзы установлены на расстоянии друг от друга, тогда, как легко найти по чертежу, точка
друг от друга, тогда, как легко найти по чертежу, точка 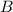 падения пучка на поверхность отрицательной линзы, отстоит от оптической оси на расстояние:
падения пучка на поверхность отрицательной линзы, отстоит от оптической оси на расстояние:
Будем считать, что данный пучок между линзами направлен в некоторую точку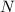 фокальной плоскости отрицательной линзы. После вторичного преломления в отрицательной линзе пучок отклонится от этой точки вверх.
фокальной плоскости отрицательной линзы. После вторичного преломления в отрицательной линзе пучок отклонится от этой точки вверх.
Проведём воображаемый луч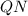 через главный оптический центр отрицательной линзы. По правилам построения изображения в тонких линзах, пучок света сразу после преломления отрицательной линзой, направится параллельно построенному воображаемому лучу. Отсюда мы можем найти угол
через главный оптический центр отрицательной линзы. По правилам построения изображения в тонких линзах, пучок света сразу после преломления отрицательной линзой, направится параллельно построенному воображаемому лучу. Отсюда мы можем найти угол 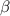 , полного преломления пучка по прохождении света через обе линзы:
, полного преломления пучка по прохождении света через обе линзы:
Отсюда хорошо видно, что если мы направим широкий параллельный пучок на положительную линзу под некоторым углом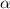 к главной оптической оси, с разными по ширине пучка значениями вертикальной координаты точки падения
к главной оптической оси, с разными по ширине пучка значениями вертикальной координаты точки падения 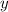 , то угол преломления по прохождении через обе линзы окажется независимым от координаты
, то угол преломления по прохождении через обе линзы окажется независимым от координаты 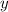 лишь в том случае, когда выполняется условие:
лишь в том случае, когда выполняется условие:
Т.е., короче говоря, правые фокусы положительной и отрицательной линзы должны быть точно совмещены, тогда любые параллельные лучи слева после преломления окажутся параллельными и справа.
Вообще, это рассуждение так же верно и для случая:
В обоих случаях мы получим телескоп или микроскоп! В случае с положительными линзами – классическую схему, а в случае с правой отрицательной – схему Ньютона.