Как изменяется внутричерепное давление при деформации костей черепа при ударе? 2. Можно ли утверждать, что удар по любой части головы опасен для всего головного мозга?
, где сила Архимеда , ρ₁ - плотность воды, V₁ - объем погруженной части тела, P - вес тела.
Для одной льдины закон Архимеда:
(1) , здесь ρ₁ - плотность воды, m₂ - масса льда, ρ₂ - плотность льда, S - площадь горизонального сечения льдины, h₁ - глубина погружения льдины в воду, h - высота льдины.
Отсюда: (2) см
Для льдины с медным кубиком:
(3) , m₂ - масса льда, m₃ - масса медного кубика, h₂ - глубина погружения льдины в воду с установленным медным кубиком.
Подставляем сюда вместо m₂ выражение 1, получаем:
(4) , где h₂-h₁ =Δh
Теперь запишем закон Архимеда для льдины с железным кубиком:
, m₂ - масса льда, m₄ - масса железного кубика, H - глубина погружения льдины в воду с установленным железным кубиком.
Подставляем сюда выражение 1:
(5) .
Выразим массу железного кубика через массу медного:
, a - длина ребра куба, ρ₄ - плотность железа.
, тогда:
(6)
Подставляя (6), (4) в (5):
Упрощая это выражение и подставляя из (2) значение h₁:
ответ:Обозначим число мелких капель через n. Тогда общая поверхность всех мелких капель
S1=4пиr^2n
Поверхность одной большой капли
S2=4пиR^2
Поверхностная энергия всех мелких капель
Un1=σ×4пиr^2n
а одной крупной капли
Un2=σ×4пиR^2
Так как температура не изменялась, то кинетическая энергия молекул воды тоже не изменилась. Следовательно, выделение энергии произошло за счет уменьшения потенциальной (поверхностной)энергии:
Q=Un1-Un2=4пиσ(r^2n-R^2)
Чтобы найти число капель n, учтем, что объем воды не изменился. Сумма объе�ов мелких капель
57,5 см
Объяснение:
Закон Архимеда:
Для одной льдины закон Архимеда:
(1)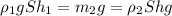 , здесь ρ₁ - плотность воды, m₂ - масса льда, ρ₂ - плотность льда, S - площадь горизонального сечения льдины, h₁ - глубина погружения льдины в воду, h - высота льдины.
, здесь ρ₁ - плотность воды, m₂ - масса льда, ρ₂ - плотность льда, S - площадь горизонального сечения льдины, h₁ - глубина погружения льдины в воду, h - высота льдины.
Отсюда: (2)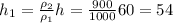 см
см
Для льдины с медным кубиком:
(3)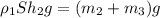 , m₂ - масса льда, m₃ - масса медного кубика, h₂ - глубина погружения льдины в воду с установленным медным кубиком.
, m₂ - масса льда, m₃ - масса медного кубика, h₂ - глубина погружения льдины в воду с установленным медным кубиком.
Подставляем сюда вместо m₂ выражение 1, получаем:
(4)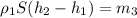 , где h₂-h₁ =Δh
, где h₂-h₁ =Δh
Теперь запишем закон Архимеда для льдины с железным кубиком:
Подставляем сюда выражение 1:
(5)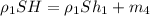 .
.
Выразим массу железного кубика через массу медного:
(6)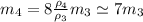
Подставляя (6), (4) в (5):
Упрощая это выражение и подставляя из (2) значение h₁:
ответ:Обозначим число мелких капель через n. Тогда общая поверхность всех мелких капель
S1=4пиr^2n
Поверхность одной большой капли
S2=4пиR^2
Поверхностная энергия всех мелких капель
Un1=σ×4пиr^2n
а одной крупной капли
Un2=σ×4пиR^2
Так как температура не изменялась, то кинетическая энергия молекул воды тоже не изменилась. Следовательно, выделение энергии произошло за счет уменьшения потенциальной (поверхностной)энергии:
Q=Un1-Un2=4пиσ(r^2n-R^2)
Чтобы найти число капель n, учтем, что объем воды не изменился. Сумма объе�ов мелких капель
V1=4/3пиr^3n
а объем большой капли
V2=4/3пиR^3
Так как V1 = V2, то
4/3пиr^3n=4/3пиR^3
Отсюда число мелких капель
n=R^3/r^3
Подставляя это значение n в выражение, получим
Q=4пиR^2×σ(R/r-1)=3.5×10^-3 Дж.
Подробнее - на -
Объяснение: