Линза рассеивающая, поскольку изображение не перевёрнутое. А раз так, то оно является мнимым, и расстояние от изображения до линзы тоже мнимое. Мнимым является и фокус рассеивающей линзы.
Расстояние от линзы до изображения равно f, а от линзы до предмета - d, но т.к. между предметом и изображением расстояние равно L и оба они находятся по одну сторону от линзы, то:
f = d - L
Однако, учитывая, что f у рассеивающей линзы - величина мнимая, возьмём её под знак модуля:
|f| = d - L
Выразим f из формулы линейного увеличения линзы:
Г = H/h = f/d => f = Hd/h => |f| = Hd/h
Приравняем выражения для |f|:
d - L = Hd/h
d - L = d*(H/h)
d - d*(H/h) = L
d*(1 - H/h) = L
d = L : (1 - H/h) = 50 : (1 - 3,2/4) = 50 : (1 - 0,8) = 50 : 0,2 = 250 см
Мы знаем, что массы у них одинаковые, а плотности разные, а это значит, что и объемы тел будут разными.
Можно просто запомнить: чем больше плотность, тем меньше сила Архимеда
Выводится это очень просто
Формула для силы Архимеда: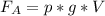
(p - плотность жидкости, V - объем погруженной части тела)
Плотность жидкости у нас одинаковая, ускорение свободного падения тоже, значит всё зависит от объема
Формула для нахождения объема: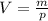
(p - плотность материала)
Мы знаем, чем больше знаменатель, тем меньше сама дробь.
И приходим к тому, что наше суждение выше было верным. Чем больше плотность, тем меньше объем.
Вернемся к нашей задаче, нам нужна наибольшая сила Архимеда, а значит, что p нам нужна минимальная, а это алюминий
ответ: На алюминиевую гирю действует большая сила Архимеда
Дано:
h = 4 см
L = 50 см
H = 3,2 см
d - ?
Линза рассеивающая, поскольку изображение не перевёрнутое. А раз так, то оно является мнимым, и расстояние от изображения до линзы тоже мнимое. Мнимым является и фокус рассеивающей линзы.
Расстояние от линзы до изображения равно f, а от линзы до предмета - d, но т.к. между предметом и изображением расстояние равно L и оба они находятся по одну сторону от линзы, то:
f = d - L
Однако, учитывая, что f у рассеивающей линзы - величина мнимая, возьмём её под знак модуля:
|f| = d - L
Выразим f из формулы линейного увеличения линзы:
Г = H/h = f/d => f = Hd/h => |f| = Hd/h
Приравняем выражения для |f|:
d - L = Hd/h
d - L = d*(H/h)
d - d*(H/h) = L
d*(1 - H/h) = L
d = L : (1 - H/h) = 50 : (1 - 3,2/4) = 50 : (1 - 0,8) = 50 : 0,2 = 250 см
ответ: 250 см.