Левая сторона 1. При выстреле пулей массой 20 г она равна 4600 Дж. имеет кинетическую энергию Какова скорость? 2. Боинг 777 на высоте 12 км над землей. 16,5*109 Дж при высотном полете потенциальная энергия. самолета Определите массу. 3. Подъемная машина Мощность двигателя 4 кВт. Он достиг высоты 15 метров за 2 минуты. может нести любую нагрузку. 4. Прежде чем воздушные шары столкнутся Чему равны импульсы
Проще всего вначале вычислить не работу силы , действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сила давления газа, действуя на поршень с силой . согласно третьему закону ньютона . модуль силы, действующей со стороны газа на поршень, равен , где p - давление газа, а s - площадь поверхности поршня. пусть газ расширяется изобарно и поршень смещается в направлении силы на малое расстояние . так как давление газа постоянно, то работа газа равна: эту работу можно выразить через изменение объема газа. начальный его объем v1=sh1, а конечныйv2=sh2. поэтому где - изменение объема газа. при расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня .
Немного неоднозначная задача, нужно найти кинетическую и потенциальную энергию, хотя не сказано с какого именно положения нужно вести отсчет времени. Я выберу это положение сам.
И еще вопрос, что понимается под амплитудой колебаний? Пусть это будет максимальной высотой подъема тела (#)
По закону сохранения энергии
(*)
где
h - амплитуда, т.е. максимальная высота подъема качели
x(t) - высота качели как ф-я времени
x'(t) - соотв. скорость качели как ф-я времени
(таким образом в правой части имеем потенциальную и кинетическую энергии)
Поставим начальное условие x(0)=0, т.е. пусть в начальный момент времени человек находился в самой нижней точке с макс. кинетической энергией.
Решим ОДУ (*) методом разделения переменных, получим в качестве решения ф-ии
из этих ф-ий выберем ту что с плюсом, т.к. именно ее производная при обращается в нуль, что соответствует моменту остановки качели по достижении макс высоты. Найдем когда именно скорость равна нулю:
отсюда
Стоит отметить, что это решение описывает движение качели лишь на интервале времени от 0 до половины периода. Но этого нам достаточно, ибо требуется найти энергии при t = 1/12 T (где T-период)
Таким образом значение нам теперь известно. Тогда
Значит качели в момент времени были на высоте
Отсюда потенциальная энергия
(Дж)
И кинетическая энергия
(Дж)
(#) Задачу можно рассматривать и как задачу гармонического осциллятора, т.е. с потенциальной энергией вида заместо типичной В этом случае данная в условии задачи частота будет использоваться (чтоб найти омега) В то же время решение ОДУ будет посложнее, функция сведется к тангенсу или чему-то подобному.
Как именно интерпретировать задачу зависит от интерпретации слова амплитуда. Я выбрал самый простой случай и что-то решил, вполне возможно совсем не то, что хотели бы видеть авторы задачи.
Немного неоднозначная задача, нужно найти кинетическую и потенциальную энергию, хотя не сказано с какого именно положения нужно вести отсчет времени. Я выберу это положение сам.
И еще вопрос, что понимается под амплитудой колебаний? Пусть это будет максимальной высотой подъема тела (#)
По закону сохранения энергии
где
h - амплитуда, т.е. максимальная высота подъема качели
x(t) - высота качели как ф-я времени
x'(t) - соотв. скорость качели как ф-я времени
(таким образом в правой части имеем потенциальную и кинетическую энергии)
Поставим начальное условие x(0)=0, т.е. пусть в начальный момент времени человек находился в самой нижней точке с макс. кинетической энергией.
Решим ОДУ (*) методом разделения переменных, получим в качестве решения ф-ии
из этих ф-ий выберем ту что с плюсом, т.к. именно ее производная при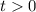 обращается в нуль, что соответствует моменту остановки качели по достижении макс высоты. Найдем когда именно скорость равна нулю:
обращается в нуль, что соответствует моменту остановки качели по достижении макс высоты. Найдем когда именно скорость равна нулю:
отсюда
Стоит отметить, что это решение описывает движение качели лишь на интервале времени от 0 до половины периода. Но этого нам достаточно, ибо требуется найти энергии при t = 1/12 T (где T-период)
Таким образом значение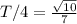 нам теперь известно. Тогда
нам теперь известно. Тогда 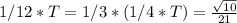
Значит качели в момент времени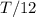 были на высоте
были на высоте 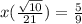
Отсюда потенциальная энергия
И кинетическая энергия
(#) Задачу можно рассматривать и как задачу гармонического осциллятора, т.е. с потенциальной энергией вида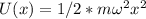 заместо типичной
заместо типичной 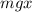 В этом случае данная в условии задачи частота будет использоваться (чтоб найти омега) В то же время решение ОДУ будет посложнее, функция сведется к тангенсу или чему-то подобному.
В этом случае данная в условии задачи частота будет использоваться (чтоб найти омега) В то же время решение ОДУ будет посложнее, функция сведется к тангенсу или чему-то подобному.
Как именно интерпретировать задачу зависит от интерпретации слова амплитуда. Я выбрал самый простой случай и что-то решил, вполне возможно совсем не то, что хотели бы видеть авторы задачи.