Невесомость наступает тогда, когда на ракету действует только сила тяжести. В таком случае вес "выключается", потому что тяготение одинаково действует и на ракету, и на всё, что внутри неё. Вес - это сила воздействия тела на опору или подвес. Но вся ракета падает, и поэтому никакой предмет внутри неё никакого действия на опору оказывать не будет.
Поэтому, если сопротивление воздуха не учитывать, то правильный ответ - от момента выключения двигателей до момента контакта с землёй. От t2 до t4.
1.
Дано: Решение:
m=20т=20000кг; F=k*x;
ΔL=x=8см=0.008м; F=m*a ⇒ a=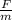 ;
;
k=50000 Н/м; a=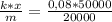 =0,2 м/с².
=0,2 м/с².
Найти: a-?
2.
Проекция силы на горизонтальную ось: Fₓ = F·cosα = 12·cos 60° = 12·(1/2) = 6 Н
Сила трения: Fтр = μ·m·g = 0,3·10·m = 3·m
Поскольку тело движется равномерно, то:
Fтр = Fₓ;
3·m = 6;
m = 6/3 = 2 кг.
3.
Дано:
P = 15 кН = 15 000 Н
R = 100 м
m = 1 т = 1000 кг
____________
V — ?
Из формулы:
P = m·(g+a)
g+a = P/m
a = P/m — g = 15000/1000 — 10 = 15-10 = 5 м/с²
Далее из формулы:
a = V²/R
V = √ (a·R) = √ (5·100) ≈ 22 м/с или V ≈ 80 км/ч
Поэтому, если сопротивление воздуха не учитывать, то правильный ответ - от момента выключения двигателей до момента контакта с землёй. От t2 до t4.
Ответ: 2)на этапе 2 и на этапе 4