, и значит, в А потенциал ближе к B, чем к С, и в то же время , а значит, в центре потенциал ближе к C, чем к B. Т.е. в А потенциал выше, чем в центре, а значит, из A в центр течёт положительный ток.
Пусть через течёт .
Пусть через течёт , тогда через течёт .
Все дальнейшие выкладки ведутся в системе СИ, в вольтах, амперах и омах, без постоянного их упоминания.
А общее падение напряжения от B к C через A составит:
;
Пусть через течёт , тогда через течёт .
А общее падение напряжения от B к C через центр составит:
;
Получаем уравнение:
;
;
;
(*) ;
На падает напряжение ;
На падает напряжение ;
При этом понятно, что на падение напряжение больше (в центре более низкий потенциал, чем в А) на величину
Отсюда получаем второе уравнение: ;
(**) ;
Решаем систему, вычитая из утроенного (*) одно (**):
;
;
, из (*);
Общее падение напряжения от B к C составляет:
;
Из точки B вытекают токи и ещё ток ;
Общий ток из B в C:
;
Полное сопротивление цепи составит:
;
Ом.
* Если бы ток был направлен в другую сторону, то оказалось бы, что , тогда общий ток должен был бы выражалтья через отрицательный коэффициент от , ну, а поскольку , то, с самого начала, мы выбрали удачное направление для . Хотя, будь он и отрицательным (при других параметрах), это ничего бы принципиально не изменило в решении. Просто в конце концов, мы поделили бы одно алгебраическое выражение с минусом на другое выражение с минусом, и так же получили бы какое-то положительное выражение для общего сопротивления.
Объяснение:
Пусть через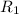
течёт 
.
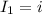Пусть через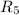
течёт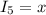 
, тогда через 
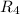течёт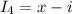 
.
Все дальнейшие выкладки ведутся в системе СИ, в вольтах, амперах и омах, без постоянного их упоминания.
А общее падение напряжения от B к C через A составит:
Пусть через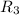
течёт 
, тогда через 
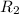течёт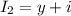 
.
А общее падение напряжения от B к C через центр составит:
Получаем уравнение:
(*)
;
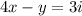На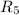
падает напряжение 
;
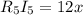На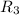
падает напряжение 
;
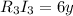При этом понятно, что на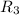
падение напряжение больше (в центре более низкий потенциал, чем в А) на величину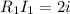 
Отсюда получаем второе уравнение: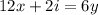
;
(**)
;
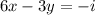Решаем систему, вычитая из утроенного (*) одно (**):
Общее падение напряжения от B к C составляет:
Из точки B вытекают токи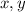
и ещё ток 
;
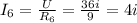Общий ток из B в C:
Полное сопротивление цепи составит:
* Если бы ток
был направлен в другую сторону, то оказалось бы, что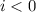 
, тогда общий ток 
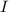должен был бы выражалтья через отрицательный коэффициент от 
, ну, а поскольку 
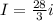, то, с самого начала, мы выбрали удачное направление для 
. Хотя, будь он и отрицательным (при других параметрах), это ничего бы принципиально не изменило в решении. Просто в конце концов, мы поделили бы одно алгебраическое выражение с минусом на другое выражение с минусом, и так же получили бы какое-то положительное выражение для общего сопротивления.
Объяснение:
Задача 1
V₀ = 36 км/ч = 10 м/м
V = 0
S = 62,5 см = 0,625 м
_________________________
n - ?
Из формулы:
S = (V²-V₀²) / (2·a)
Ускорение:
a = (V²-V₀²) / (2·S) = (0² - 10²)/(2·0,625) = - 80 м/с²
Ускорение отрицательное, поскольку происходило торможение.
Перегрузка (по модулю):
n = a / g = 80 / 10 = 8
Восьмикратная перегрузка.
Задача 2
m = 1,6 кг
k = 400 Н/м
μ = 0,3
___________
Δx - ?
Составим уравнение:
k·Δx = μ·m·g
Δx = μ·m·g / k = 0,3·1,6·10/40 = 0,12 м или 12 см
Задача 3
M = 150 г = 0,15 кг
d₁ = d/4
_____________
Mлин - ?
Сделаем чертеж.
Разделим линейку на 8 единичных частей.
Пусть масса 1 части равна m.
Составим условие равновесия:
F₁·L₁ = F₂·L₂+P·L
(6·m·g)·3 = (2·m·g)·1 + Mg·2
18m = 2·m + 0,150·2/g
16m = 3/10
m=3/160
Но масса всей линейки в 8 раз больше:
Mлинейки = 8·3/160 = 0,15 кг