Около речной пристани канатом длиной 8 метров привязана баржа с углем. Со стороны течения реки на нее действует сила, направленная параллельно пристани и равная 520 Н. Кроме того, так как погода портится, то возникает сильный ветер, который дует с берега, где расположена пристань перпендикулярно реке и действует на баржу с силой 187 Н. С какой силой баржа натягивает канат? На каком расстоянии от берега (по кратчайшему отрезку) располагается крепление каната к барже?
M = - 1,25 - 3,001*lg5 = - 3,35^m
с другой стороны
M = m + 5 - 5*lg(r)? r - расстояние до цефеиды в парсеках (пк)
- 3,35 = 15 + 5 - 5*lg(r)
lg(r) = (15 + 5 + 3,35) / 5 = 23,35 / = 4,67
r = 10^4,67 = 46774 пк
2) P = 0,12/√ρ =
P - период пульсации цефеиды (в сутках)
ρ - средняя плотность цефеиды (в единицах средней плотности Солнца) = 1408 кг/м³
ρ = 0,0144 / Р² = 0,0144/20² = 3,6*10⁵*1408 кг/м³ ≈ 5,07*10⁻² кг/м³
3) Видимая звездная величина Солнца m = - 26,8^m
r = 1 а. е. = 1/206265 пк
M = m + 5 - 5*lg(r) = - 26,8 + 5 - 5*lg(1/206265) = - 26,8 + 5 + 26,6 =
= 4,8^m
4) υ = S / t = 150000000 км / (3*24*3600 с ) = 579 км/с
ответ: Никак не измениться
Объяснение:
Пусть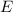
- напряжённость электростатического поля создаваемым точечным зарядом 
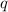. В некоторую точку этого электростатического поля помещают пробный заряд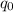 
По определению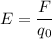
Где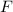
- сила электростатического взаимодействия между двумя точечными зарядами 
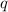и 
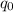
Согласно закону Кулона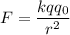
Где
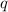- расстояние между точечными зарядами 
и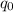 
Преобразуем первую формулу
Как видно из итоговой формулы напряженность электростатического поля создаваемым точечным зарядом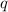
никак не зависит от значения модуля пробного заряда внесенного в это поле.
В принципе формулу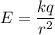
можно было записать и самого начала и объяснить что так и так. Или даже вовсе не записывать и все объяснить словами.