Задача на момент силы. В общем, считается, что палка находится в равновесии относительно человека, следовательно, сумма моментов сил должна быть равна нулю.
Поскольку на рычаг действуют сила тяжести груза и сила упругости и моменты этих сил противонаправленны, запишем это сразу в качестве равенства. m1- масса груза, l1 - расстояние от руки до груза, следовательно, l1=1 м.
N - сила упругости от плеча, l2 - расстояние от руки до плеча.
N*l2=m1*g*l1;
Следовательно,
Сила упругости равна силе давления палки на плечо.
ответ: 83,3(3) Н
Вот например, в чём ошибка Русакова? Он неправильно измерил плечи, ведь точкой опоры считается рука, а не плечо. Если бы точкой опоры считалось плечо, то сила давления на плечо не считалась бы через моменты сил.
управляющий стержень - Чтобы реактор не становился надкритичным, одновременно искусственно снижается k0 размножающей среды. Это достигается введением в активную зону веществ-поглотителей нейтронов, которые могут удаляться из активной зоны в последующем. Так же как и в элементах регулирования цепной реакции, вещества-поглотители входят в состав материала стержней того или иного поперечного сечения, перемещающихся по соответствующим каналам в активной зоне.
Для управления ядерным реактором служит система управления и защиты (СУЗ).
В большинстве случаев для управления реактором используют стержни, вводимые в активную зону, изготовленные из материалов, сильно поглощающих нейтроны (Cd, В и др.). Движение стержней управляется специальными механизмами, работающими по сигналам приборов, чувствительных к величине нейтронного потока.
Задача на момент силы.
В общем, считается, что палка находится в равновесии относительно человека, следовательно, сумма моментов сил должна быть равна нулю.
Поскольку на рычаг действуют сила тяжести груза и сила упругости и моменты этих сил противонаправленны, запишем это сразу в качестве равенства.
m1- масса груза, l1 - расстояние от руки до груза, следовательно, l1=1 м.
N - сила упругости от плеча, l2 - расстояние от руки до плеча.
N*l2=m1*g*l1;
Следовательно,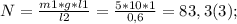
Сила упругости равна силе давления палки на плечо.
ответ: 83,3(3) Н
Вот например, в чём ошибка Русакова? Он неправильно измерил плечи, ведь точкой опоры считается рука, а не плечо.
Если бы точкой опоры считалось плечо, то сила давления на плечо не считалась бы через моменты сил.
управляющий стержень - Чтобы реактор не становился надкритичным, одновременно искусственно снижается k0 размножающей среды. Это достигается введением в активную зону веществ-поглотителей нейтронов, которые могут удаляться из активной зоны в последующем. Так же как и в элементах регулирования цепной реакции, вещества-поглотители входят в состав материала стержней того или иного поперечного сечения, перемещающихся по соответствующим каналам в активной зоне.
Для управления ядерным реактором служит система управления и защиты (СУЗ).
В большинстве случаев для управления реактором используют стержни, вводимые в активную зону, изготовленные из материалов, сильно поглощающих нейтроны (Cd, В и др.). Движение стержней управляется специальными механизмами, работающими по сигналам приборов, чувствительных к величине нейтронного потока.