Расстояние от освещенного предмета до экрана 1м. Линза,помещенная между предметом и экраном,даёт чёткое изображение предмета на экране при двух положениях,расстояние между которыми 20 см. Найти фокусное расстояние линзы.

В задачах части «С» необходимо описывать все параметры, которых нет в дано, иначе оценку снижают на один .

Поэтому пишем:

L – расстояние по горизонтали между первым и вторым ударами о плоскость.

Нарисуем наклонную плоскость и начальную скорость шарика \overrightarrow{\mkern -5mu V_0}. Как известно из геометрии, углы с перпендикулярными сторонами равны. Начальная скорость шарика перпендикулярна основанию наклонной плоскости. Восстановим перпендикуляр к наклонной плоскости в точке падения на нее шарика. Тогда угол между этим перпендикуляром и вектором начальной скорости равен углу наклона плоскости к горизонту (углы с перпендикулярными сторонами, зеленые пунктирные линии на рисунке). Угол падения шарика (с перпендикуляром) равен углу отражения \alpha = 30^{\circ}. Тогда угол между начальной скоростью отскочившего шарика и наклонной плоскостью равен \beta = 90^{\circ} - \alpha = 90^{\circ} - 30^{\circ} = 60^{\circ} = 2 \alpha. Модуль скорости не меняется, так как удар упругий.

Объяснение:

Дано:

Идеальный колебательный контур

L = 0,45 мГн = 0, 45 ×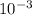

Найти:

1) I max - ? А     T - ? с

2) ν - ? Гц          ω - ?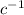

3) Ур-е колебания I - ?

1) Найдём нужные величины из графика.

Максимальная сила тока равна амплитуде силы тока.

I max = 6 мА = 6 ×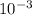 А

Период - время, за которое один полный цикл колебаний.

T = 6 мкс = 6 ×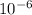

2) Частота - величина, обратная периоду.

ν = = = 0,1(6) × ≈ 0,17 ×

Циклическая частота - частота колебаний за 2π секунд.

ω = 2πν = 2 × 3,14 × 0,17 × ≈ 1,07 ×

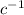
3) I = I max × Sin ωt

I = 6 ×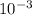 × Sin (1,07 × t)

Таким образом, индуктивность катушки в задаче - лишние данные.