Я ранее отвечала на этот вопрос. И отвечу снова. За счёт того, как свет падает на предмет. Просто разные тела по-разному поглощают свет. Если цвет предмета белый, то большая часть света отражается от предмета. (т.е предмет отражает свет)
Если чёрный - то поглощает в себя. А есть стекло, оно пропускает через себя свет, поэтому оно и прозрачное. Если цвет предмета, например, красный, то это означает, что больше света в диапазоне красного цвета отражается, а в остальных диапазонах он поглощается. Если бы все предметы пропускали через себя свет, мы бы ничего вокруг себя не видели.
Мгновенный центр вращения квадрата располагается на перпендикуляре к скорости v, а значит лежит на прямой AD. Известно, что угловая скорость вращения ω =4 рад/c. Чтобы найти скорость v, нужно умножить расстояние от центра вращения на угловую скорость вращения. Определим расстояние от центра вращения:
x = = 0.25м
Заметим, что это расстояние в точности равно стороне квадрата. Известно, что скорость v направлена к точке В, а также, что направление обхода вершин квадрата совпадает с направлением его вращения. Это значит, что из двух точек лежащих на прямой AD, нам подходит только точка D => точка D является мгновенным центром вращения и ее скорость равна 0.
Я ранее отвечала на этот вопрос. И отвечу снова. За счёт того, как свет падает на предмет. Просто разные тела по-разному поглощают свет. Если цвет предмета белый, то большая часть света отражается от предмета. (т.е предмет отражает свет)
Если чёрный - то поглощает в себя. А есть стекло, оно пропускает через себя свет, поэтому оно и прозрачное. Если цвет предмета, например, красный, то это означает, что больше света в диапазоне красного цвета отражается, а в остальных диапазонах он поглощается. Если бы все предметы пропускали через себя свет, мы бы ничего вокруг себя не видели.
ответ: 1.4м/c 1м/c 1м/c 0м/c
Объяснение:
Мгновенный центр вращения квадрата располагается на перпендикуляре к скорости v, а значит лежит на прямой AD. Известно, что угловая скорость вращения ω =4 рад/c. Чтобы найти скорость v, нужно умножить расстояние от центра вращения на угловую скорость вращения. Определим расстояние от центра вращения:
x =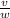
= 0.25м
Заметим, что это расстояние в точности равно стороне квадрата. Известно, что скорость v направлена к точке В, а также, что направление обхода вершин квадрата совпадает с направлением его вращения. Это значит, что из двух точек лежащих на прямой AD, нам подходит только точка D => точка D является мгновенным центром вращения и ее скорость равна 0.
Теперь легко определяем скорости точек C и B:
Vc = ωa = 1м/c
Vb = ω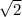
a = 1.4 м/c