с пружины с коэффициентом жесткости 50 ньютон на метр тянут по поверхности стола брусок коэффициент трения которого равен 0.2. найти массу бруска если пружина растягивается на 2 см

Согласно условию скорость зависит от угла поворота $v(\phi)=\frac{\phi}{2\pi}*V$

Нормально ускорение: $a_n=\frac{v^2}{R}$

а) $\phi=2\pi$ $a_n=\frac{V^2}{R}$

б) $\phi=\pi$ $v(\phi)=\frac{\pi}{2\pi}*V=\frac{V}{2}$ $a_n=\frac{V^2}{4R}$

в) $\phi=\frac{\pi}{2}$ $v(\phi)=\frac{\frac{pi}{2}}{2\pi}*V=\frac{V}{4}$

$a_n=\frac{V^2}{16R}$

г) $\phi=\frac{\pi}{3}$ $v(\phi)=\frac{\frac{pi}{3}}{2\pi}*V=\frac{V}{6}$

$a_n=\frac{V^2}{36R}$

д) $\phi=0$ $a_n=0$

Тангенциальное ускорение:

Поскольку ни период, ни время, ни частота оборотов в условии не заданы, определить тангенциальное ускорение в метрах за секунду в квадрате не представляется возможным. Ничего не остаётся, как привязать это ускорение к углу поворота, тогда у нас будут единицы м/(рад*с)

Тангенциальное ускорение $a_{tau}=\frac{V-0}{2\pi}=\frac{V}{2\pi}$

Оно будет постоянным для всего оборота $a_{tau}=\frac{V}{2*3,14}\approx 0,16V$

а) $\phi=2\pi$ $a_{tau}\approx 0,16V$

б) $\phi=\pi$ $a_{tau}\approx 0,16V$

в) $\phi=\frac{\pi}{2}$ $a_{tau}\approx 0,16V$

г) $\phi=\frac{\pi}{3}$ $a_{tau}\approx 0,16V$

д) $\phi=0$ $a_{tau}\approx 0,16V$

Полное ускорение: $a=\sqrt{a_n^2+a_{\tau}^2}$

а) $\phi=2\pi$ $a=\sqrt{(\frac{V^2}{R})^2+(0,16V)^2}$

б) $\phi=\pi$ $a=\sqrt{(\frac{V^2}{4R})^2+(0,16V)^2}$

в) $\phi=\frac{\pi}{2}$ $a=\sqrt{(\frac{V^2}{16R})^2+(0,16V)^2}$

г) $\phi=\frac{\pi}{3}$ $a=\sqrt{(\frac{V^2}{36R})^2+(0,16V)^2}$

д) $\phi=0$ $a=\sqrt{(0,16V)^2}=0,16V$

ответ: за 98 секунд

Объяснение:

Запишем «Дано»:

N = 1,5 кВт = 1500 Вт

Vв = 500 л =>

=> mв = 500 кг

h = 30 м

Чтобы поднять 500 кг воды на высоту 30 м, насос должен совершить работу, которую можно вычислить по формуле

А = F*S = m*g*S, где

F — сила, которую нужно приложить для поднятия воды, m — масса воды, g — ускорение свободного падения, S — перемещение воды (в данном случае оно равно высоте поднятия воды h).

!Вообще формула работы записывается как А = FS*cos a, где а — угол между направлениями F и S. Если эту формулу ещё не проходили, нужно сразу использовать формулу без cos a. Если проходили, нужно уточнить, что в данном случае F сонаправлено с S, a = 0°, cos a = 1, а значит, формула записывается как А = FS*1 = FS !

Работа, совершённая насосом, рассчитывается по формуле

А = N*t, где

N — мощность насоса,

t — время его работы.

Следовательно,

А = А

mgS = Nt, или

mgh = Nt

Выразим отсюда время:

t =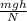

Подставим значения:

t =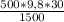 = 98 (с)