сани тянут по горизонтальной поверхности с верёвки которая образует с поверхностью угол 30 градусов. силы натяжения веревки 20Н. Определите работу силы натяжения при перемещении саней на расстоянии 5м
длина волны, скорость волны, период колебаний, частота колебаний.
Объяснение:
Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.
Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.
Поскольку скорость волны - величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней: λ=υT. Так как период Т и частота v связаны соотношением T = 1 / v, то скорость волны:
υ = λ / Т = λ v
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.
Частота - это число колебаний в единицу времени , где n - число колебаний, t - промежуток времени (с). Вычислим: Герц.
Период обратен частоте т.е. . Вычислим:
По формуле математического маятника , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем:
По формуле математического маятника , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период:
Частота следовательно будет равна: Гц
Используем две формулы периода , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и
Левые части формул равны, следователь и правые части также равны:
Величины, характеризующие волну:
длина волны, скорость волны, период колебаний, частота колебаний.
Объяснение:
Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.
Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.
Поскольку скорость волны - величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней: λ=υT. Так как период Т и частота v связаны соотношением T = 1 / v, то скорость волны:
υ = λ / Т = λ v
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.
Частота - это число колебаний в единицу времени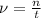 , где n - число колебаний, t - промежуток времени (с). Вычислим:
, где n - число колебаний, t - промежуток времени (с). Вычислим: 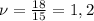 Герц.
Герц.
Период обратен частоте т.е.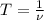 . Вычислим:
. Вычислим: 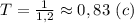
По формуле математического маятника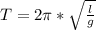 , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем:
, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем: 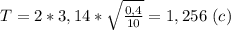
По формуле математического маятника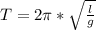 , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период:
, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период: 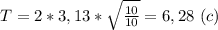
Частота следовательно будет равна: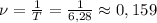 Гц
Гц
Используем две формулы периода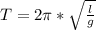 , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и
, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и 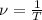
Левые части формул равны, следователь и правые части также равны:
Распишем частоту: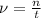
Подставляем и вычисляем: