В изобарном процессе при давлении p=80 кПа абсолютная температура идеального газа увеличилась на 40%. Определите начальный объём газа, если при расширении силой давления газа совершена работа А=160 Дж.
Дано: m = 1 кг υ₀ = 10 м/с h = 1,8 м g ≈ 10 м/с² ───────── F = ?
Решение: Изменение импульса тела постоянной массы может происходить, только в результате изменения скорости и всегда обусловлено действием силы: Δp = m·υ = F·Δt Получаем соотношение: m·υ = F·Δt где υ - скорость тела, после времени Δt на высоте h. Время поднятия на высоту h находим из соотношения: h = υ₀·t - 0,5·g·t² 0,5·g·t² - υ₀·t + h = 0 0,5·10·t² - 10·t + 1,8 = 0 5·t² - 10·t + 1,8 = 0 - решаем квадратное ур-ние D = 10² - 4·5·1,8 = 64 -10 + √64 -10 - √64 t₁ = ─────── = - 0,2 t₂ = ─────── = - 1,8 2·5 2·5 Получили два корня: t₁ = 0,2 и t₂ = 1,8 c Скорость у самой горизонтальной преграды после времени t₍₁₋₂₎: υ₁ = υ₀ - g·t₁ = 10 - 10·0,2 = 8 (м/с) υ₂ = υ₀ - g·t₂ = 10 - 10·1,8 = -8 (м/с) - второй корень отпадает т.к. скорость отрицательной быть не может (по величине). Определяем силу импульса: m · υ 1 · 8 F = ───── = ───── = 40 (Н) Δt 0,2 Импульс силы будет: Δp = F · t = 40 · 0,2 = 8 (Н·с)
№1. а) сила Архимеда одинакова (она определяется объемом погруженного в жидкость тела); б) так как плотность меди больше плотности алюминия, объем медного шара равной массы будет меньше, соответственно сила Архимеда, действующая на него будет меньше.
№2. С гидростатического взвешивания измеряют плотности твердых тел и жидкостей. В первом случае твердое тело взвешивают в воздухе и в жидкости, определяя массу и объем, соответственно, а потом деля одно на другое. Во втором - берут тело известной массы и объема, взвешивают его в жидкости, определяя силу Архимеда, а затем плотность жидкости.
№3. Если взять плотность гранита 2600 кг/м^3, то объем камня равен 0.0038 м^3, а сила Архимеда, действующая на него = 38 Н ( = 1000 кг/м^3 - плотность воды). Вычитая из силы тяжести (mg=10 кг*9.8 м/с^2 = 98 Н) силу Архимеда получим силу, которую надо приложить, чтобы поднять камень, 60 Н.
m = 1 кг
υ₀ = 10 м/с
h = 1,8 м
g ≈ 10 м/с²
─────────
F = ?
Решение:
Изменение импульса тела постоянной массы может происходить, только в результате изменения скорости и всегда обусловлено действием силы:
Δp = m·υ = F·Δt
Получаем соотношение:
m·υ = F·Δt
где υ - скорость тела, после времени Δt на высоте h.
Время поднятия на высоту h находим из соотношения:
h = υ₀·t - 0,5·g·t²
0,5·g·t² - υ₀·t + h = 0
0,5·10·t² - 10·t + 1,8 = 0
5·t² - 10·t + 1,8 = 0 - решаем квадратное ур-ние
D = 10² - 4·5·1,8 = 64
-10 + √64 -10 - √64
t₁ = ─────── = - 0,2 t₂ = ─────── = - 1,8
2·5 2·5
Получили два корня: t₁ = 0,2 и t₂ = 1,8 c
Скорость у самой горизонтальной преграды после времени t₍₁₋₂₎:
υ₁ = υ₀ - g·t₁ = 10 - 10·0,2 = 8 (м/с)
υ₂ = υ₀ - g·t₂ = 10 - 10·1,8 = -8 (м/с) - второй корень отпадает т.к. скорость отрицательной быть не может (по величине).
Определяем силу импульса:
m · υ 1 · 8
F = ───── = ───── = 40 (Н)
Δt 0,2
Импульс силы будет:
Δp = F · t = 40 · 0,2 = 8 (Н·с)
№1. а) сила Архимеда одинакова (она определяется объемом погруженного в жидкость тела); б) так как плотность меди больше плотности алюминия, объем медного шара равной массы будет меньше, соответственно сила Архимеда, действующая на него будет меньше.
№2. С гидростатического взвешивания измеряют плотности твердых тел и жидкостей. В первом случае твердое тело взвешивают в воздухе и в жидкости, определяя массу и объем, соответственно, а потом деля одно на другое. Во втором - берут тело известной массы и объема, взвешивают его в жидкости, определяя силу Архимеда, а затем плотность жидкости.
№3. Если взять плотность гранита 2600 кг/м^3, то объем камня равен 0.0038 м^3, а сила Архимеда, действующая на него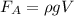
= 38 Н (
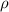= 1000 кг/м^3 - плотность воды). Вычитая из силы тяжести (mg=10 кг*9.8 м/с^2 = 98 Н) силу Архимеда получим силу, которую надо приложить, чтобы поднять камень, 60 Н.