S = 0.0225 метров
Объяснение:
Для начала зададим уравнение колебательного движения
x = Acos(ωt) где ω = 2/T , отсюда:
x = Acos(2t/T) также заметим что t здесь это переменная времени, а период это заглавная буква T
При этого уравнения мы можем узнать смещение тела в определённый момент времени.
Воспользуемся тем что за время T тело проходит путь равный 4A, отсюда вычисляем время за которое тело сдвинется на одну A:
30/4 = 7.5 секунд
Теперь узнаем сколько Амплитуд завершилось за время t:
10/7.5 = 1 и 1/3 , отмечу что нас интересует только целая часть
Чтобы узнать весь путь пройденный телом мы прибавляем к этой самой одной амплитуде сдвиг совершённый сразу после него:
S = A + Acos(2t/T)
Дальше идут вычисления:
S = 15 + 15*cos(2*10/30) = 15 + 15*cos(2/3)
S = 15 + 15*(1/2) = 22.5 мм.
Переведем миллиметры в метры и получим S = 0.0225 метров
По формуле тонкой линзы:
1/F=1/f+1/d
Где F - фокусное расстояние; f - расстояние от изображения до линзы; d - расстояние от предмета до линзы.
d=19 см. (по условию)
F=4 см. (по условию)
Найдём f:
1/4=1/19+1/f
1/f=1/4-1/19=15/76
Так как нам нужна f, а не 1/f, дробь переворачиваем:
f=76/15 см.
По формуле линейного увеличения тонкой линзы:
Г=f/d где Г - линейное увеличение тонкой линзы; f - расстояние от изображения до линзы; d - расстояние от предмета до линзы.
Г=(76/15)/19=4/15
То есть размеры изображения муравья в 4/15 меньше его самого, значит и путь он в 4/15 меньше:
V=1,2*(4/15)=0,32 см/с
ответ: 0,32 см/с
S = 0.0225 метров
Объяснение:
Для начала зададим уравнение колебательного движения
x = Acos(ωt) где ω = 2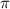 /T , отсюда:
/T , отсюда:
x = Acos(2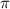 t/T) также заметим что t здесь это переменная времени, а период это заглавная буква T
t/T) также заметим что t здесь это переменная времени, а период это заглавная буква T
При этого уравнения мы можем узнать смещение тела в определённый момент времени.
Воспользуемся тем что за время T тело проходит путь равный 4A, отсюда вычисляем время за которое тело сдвинется на одну A:
30/4 = 7.5 секунд
Теперь узнаем сколько Амплитуд завершилось за время t:
10/7.5 = 1 и 1/3 , отмечу что нас интересует только целая часть
Чтобы узнать весь путь пройденный телом мы прибавляем к этой самой одной амплитуде сдвиг совершённый сразу после него:
S = A + Acos(2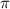 t/T)
t/T)
Дальше идут вычисления:
S = 15 + 15*cos(2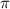 *10/30) = 15 + 15*cos(2
*10/30) = 15 + 15*cos(2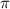 /3)
/3)
S = 15 + 15*(1/2) = 22.5 мм.
Переведем миллиметры в метры и получим S = 0.0225 метров
По формуле тонкой линзы:
1/F=1/f+1/d
Где F - фокусное расстояние; f - расстояние от изображения до линзы; d - расстояние от предмета до линзы.
d=19 см. (по условию)
F=4 см. (по условию)
Найдём f:
1/4=1/19+1/f
1/f=1/4-1/19=15/76
Так как нам нужна f, а не 1/f, дробь переворачиваем:
f=76/15 см.
По формуле линейного увеличения тонкой линзы:
Г=f/d где Г - линейное увеличение тонкой линзы; f - расстояние от изображения до линзы; d - расстояние от предмета до линзы.
Г=(76/15)/19=4/15
То есть размеры изображения муравья в 4/15 меньше его самого, значит и путь он в 4/15 меньше:
V=1,2*(4/15)=0,32 см/с
ответ: 0,32 см/с