знать совсем немного. Напомним их основные свойства.
1) Характер линзы зависит от радиусов образующих ее
сферических поверхностей и от показателя преломления
материала линзы относительно окружающей среды
n n n = л ср . При n > 1 двояковыпуклая и плосковыпуклая
линзы – собирающие, двояковогнутая и плосковогнутая
линзы – рассеивающие; при n < 1 – наоборот. Эти утверждения следуют из формулы для фокусного расстояния F:
( )
1 2
1 1 1
n 1
F R R
Ê ˆ
= - + Á ˜ Ë ¯ ,
где радиус выпуклой поверхности считается положительным, а радиус вогнутой – отрицательным. Если F положительно, то линза собирающая, в противном случае – рассеивающая. Эту формулу знать полезно, но необязательно.
Пример 1
. Из очень тонких одинаковых сферических стеклянных сегментов изготовлены линзы, представленные на рисунке 1. Если показатель преломления глицерина больше, чем показатель преломления воды, то собирающая линза представлена на рисунке: 1); 2); 3); 4).
(ответ: 4).)
2) Для решения задач полезно знать ход основных лучей.
а) Лучи, идущие через оптический центр линзы, не испытывают отклонения.
б) Лучи, падающие параллельно главной оптической оси
(рис.2), сходятся в фокусе, лежащем за линзой – в случае
, где сила Архимеда , ρ₁ - плотность воды, V₁ - объем погруженной части тела, P - вес тела.
Для одной льдины закон Архимеда:
(1) , здесь ρ₁ - плотность воды, m₂ - масса льда, ρ₂ - плотность льда, S - площадь горизонального сечения льдины, h₁ - глубина погружения льдины в воду, h - высота льдины.
Отсюда: (2) см
Для льдины с медным кубиком:
(3) , m₂ - масса льда, m₃ - масса медного кубика, h₂ - глубина погружения льдины в воду с установленным медным кубиком.
Подставляем сюда вместо m₂ выражение 1, получаем:
(4) , где h₂-h₁ =Δh
Теперь запишем закон Архимеда для льдины с железным кубиком:
, m₂ - масса льда, m₄ - масса железного кубика, H - глубина погружения льдины в воду с установленным железным кубиком.
Подставляем сюда выражение 1:
(5) .
Выразим массу железного кубика через массу медного:
, a - длина ребра куба, ρ₄ - плотность железа.
, тогда:
(6)
Подставляя (6), (4) в (5):
Упрощая это выражение и подставляя из (2) значение h₁:
ЛЯ РЕШЕНИЯ ЗАДАЧ С ТОНКИМИ ЛИНЗАМИ НАДО
знать совсем немного. Напомним их основные свойства.
1) Характер линзы зависит от радиусов образующих ее
сферических поверхностей и от показателя преломления
материала линзы относительно окружающей среды
n n n = л ср . При n > 1 двояковыпуклая и плосковыпуклая
линзы – собирающие, двояковогнутая и плосковогнутая
линзы – рассеивающие; при n < 1 – наоборот. Эти утверждения следуют из формулы для фокусного расстояния F:
( )
1 2
1 1 1
n 1
F R R
Ê ˆ
= - + Á ˜ Ë ¯ ,
где радиус выпуклой поверхности считается положительным, а радиус вогнутой – отрицательным. Если F положительно, то линза собирающая, в противном случае – рассеивающая. Эту формулу знать полезно, но необязательно.
Пример 1
. Из очень тонких одинаковых сферических стеклянных сегментов изготовлены линзы, представленные на рисунке 1. Если показатель преломления глицерина больше, чем показатель преломления воды, то собирающая линза представлена на рисунке: 1); 2); 3); 4).
(ответ: 4).)
2) Для решения задач полезно знать ход основных лучей.
а) Лучи, идущие через оптический центр линзы, не испытывают отклонения.
б) Лучи, падающие параллельно главной оптической оси
(рис.2), сходятся в фокусе, лежащем за линзой – в случае
Объяснение:
57,5 см
Объяснение:
Закон Архимеда:
Для одной льдины закон Архимеда:
(1)
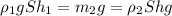, здесь ρ₁ - плотность воды, m₂ - масса льда, ρ₂ - плотность льда, S - площадь горизонального сечения льдины, h₁ - глубина погружения льдины в воду, h - высота льдины.
Отсюда: (2)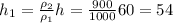
см
Для льдины с медным кубиком:
(3)
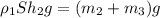, m₂ - масса льда, m₃ - масса медного кубика, h₂ - глубина погружения льдины в воду с установленным медным кубиком.
Подставляем сюда вместо m₂ выражение 1, получаем:
(4)
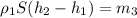, где h₂-h₁ =Δh
Теперь запишем закон Архимеда для льдины с железным кубиком:
Подставляем сюда выражение 1:
(5)
.
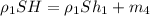Выразим массу железного кубика через массу медного:
(6)
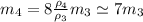
Подставляя (6), (4) в (5):
Упрощая это выражение и подставляя из (2) значение h₁: