1.(1 б).знайдіть косинус гострого кута а, якщо

sin а=12/13.

а)5/13; б) 1/13; в) – 5/13; г)-1/13.

2). (1 б). кут при вершині рівнобедреного трикутника дорівнює 120˚, а бічна сторона 3 см. знайдіть довжину радіуса описаного кола.

а) 3 см; б) 12см; в) 1 см; г ) 2 см.

3. (1 б). в авс ∠а= 46˚, ∠в= 82˚, ∠с= 51˚. вкажіть найбільшу сторону трикутника.

а) ав; б) вс; в) ас; г) визначити неможна.

Показать ответ

Ответ:

vik5611

03.05.2022 15:33

$\displaystyle 2\frac{1}{2}$ ед²

Объяснение:

Дано: ABCD - параллелограмм.

AE = ED; DF = FC.

BE ∩ AC = G; BF ∩ AC = H;

S (ABCD) = 12.

Найти: S (GHFE)

1. Рассмотрим ΔABD и ΔDBC.

Любая диагональ параллелограмма делит его на два равных треугольника.

⇒ S (ΔABD) = S (ΔDBC) = 12:2 = 6

Аналогично:

S (ΔABC) = S (ΔACD) = 12:2 = 6

2. Рассмотрим ΔABD.

AE = ED (условие) ⇒ВЕ - медиана.

Медиана делит треугольник на два равновеликих треугольника.

⇒ S (ΔABE) = S (ΔEBD) = 6:2 = 3

3. Рассмотрим ΔDBC.

DF = FC ⇒ BF - медиана.

S (ΔDBF) = S(ΔFBC) = 6:2 = 3

4. Рассмотрим ΔACD.

AE = ED; DF = FC (условие)

⇒ EF - средняя линия.

Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвертой площади исходного треугольника.

⇒ $\displaystyle S_{EFD}=\frac{1}{4}*S_{ACD} =\frac{1}{4}*6=\frac{3}{2}$

5. Найдем площадь ΔEBF.

S (ΔEBF) = S (ABCD) - S(ΔABE) - S(ΔFBC) - S(ΔEFD) =

$\displaystyle =12-6-6-\frac{3}{2}=\frac{9}{2}$

6. Рассмотрим ΔABD.

BF - медиана (п.3)

Диагонали параллелограмма точкой пересечения делятся пополам.

⇒ BO = OD ⇒ СО - медиана.

Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.

⇒ BH : HF = 2:1

или ВН : BF = 2:3

7. Рассмотрим ΔABD.

Аналогично п.6: BE и AO - медианы.

⇒BG : GE = 2 :1

или BG :BE = 2:3

8. Рассмотрим ΔGBH и ΔEBF.

∠B - общий. ВН : BF = 2:3 (п.6); BG :BE = 2:3 (п.7)

⇒ ΔGBH ~ ΔEBF, k =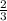 $\frac{2}{3}$

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

$\displaystyle \frac{S_{GBH}}{S_{EBF}} =k^2=\frac{4}{9}\\\\S_{GBH}=\frac{S_{EBF}*4}{9}=\frac{9*4}{2*9}=2$

Найдем площадь GHFE:

$\displaystyle S_{GHFE}=S_{EBF}-S_{GBH}=\frac{9}{2}-2=2\frac{1}{2}$

0,0(0 оценок)

Ответ:

farita1

07.04.2022 13:36

Объяснение:

$\displaystyle y=\frac{x^2-x+1}{x}$

1. ОДЗ: х≠0;

или х ∈ (-∞; 0) ∪ (0; +∞)

2. Четность, нечетность.

$\displaystyle y(-x)=\frac{(-x)^2-(-x)+1}{-x}=-\frac{x^2+x+1}{x}y(-x)\neq y(x)\neq -y(x)$

⇒ функция не является четной или нечетной, то есть - общего вида.

3. Пересечение с осями.

1) х ≠ 0 ⇒ ось 0у не пересекает.

2) у = 0 ⇒

$\displaystyle x^2-x+1=0D=1-4*1*1=-3$

⇒ корней нет, то есть ось 0х не пересекает.

4. Асимптоты.

1) Вертикальная.

$\displaystyle \lim_{x \to 0} \frac{x^2-x+1}{x}=\infty$

⇒ x=0 - вертикальная асимптота.

2) Наклонная: у = kx + b

$\displaystyle k= \lim_{x \to \infty} \frac{x^2-x+1}{x*x}= \lim_{x \to \infty} \frac{\frac{x^2}{x^2}-\frac{x}{x^2}+\frac{1}{x^2} }{\frac{x^2}{x^2} } =1b= \lim_{x \to \infty} \left(\frac{x^2-x+1}{x}-1*x\right)= \lim_{n \to \infty} \frac{x^2-x+1-x^2}{x}== \lim_{x \to \infty} \frac{-\frac{x}{x}+\frac{1}{x} }{\frac{x}{x} }=-1$

⇒ y = x - 1 - наклонная асимптота.

5. Возрастание, убывание, экстремумы.

Найдем производную, приравняем к 0, найдем корни и отметим их на числовой оси. Определим знаки производной на промежутках. Если "+" - возрастает, если "-" - убывает.

$\displaystyle y'=\frac{(2x-1)*x-(x^2-x+1)*1}{x^2} ==\frac{2x^2-x-x^2+x-1}{x^2} =\frac{x^2-1}{x^2}=\frac{(x-1)(x+1)}{x^2}x=1;\;\;\;\;\;x=-1;\;\;\;\;\;x\neq 0$