Для начала найдем гипотенузу этого треугольника. По теореме Пифагора, квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов его катетов.
см.
Теперь найдем острые углы этого треугольника. Сделаем это через их синусы. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. Пусть угол B лежит напротив катета b. Тогда .
Таким образом, ≈ 56,44°.
Зная это, мы можем найти оставшийся угол А. .
В треугольнике напротив большей стороны всегда лежит больший угол. Значит, наше утверждение правильно. Катет b больше катета a. Поэтому угол B - тот, который лежит напротив катета b, угол A - тот, что лежит напротив катета a.
∠А=100°
∠В=100°
∠D=80°
∠C=80°
Объяснение:
Дано
ABCD- равнобокая трапеция.
АD=BC
∠B-∠D=20°
∠A=?
∠B=?
∠C=?
∠D=?
Решение
В равнобокой трапеции углы при основании равны
∠D=∠C
∠A=∠B.
Пусть градусная мера угла ∠В будет х°, а градусная мера угла ∠С будет у°.
Сумма углов прилежащих к боковой стороне трапеции равна 180° (∠В+∠С=180°, свойство трапеции)
х+у=180°
А разность углов ∠В-∠D=20°, по условию.
х-у=20
Составляем систему уравнений.
{х+у=180
{х-у=20
Метод алгебраического сложения
2х=200
х=200:2
х=100° градусная мера угла ∠В, и угла ∠А
Подставляем значение х в одно из уравнений.
х+у=180
100+у=180
у=180-100
у=80° градусная мера угла ∠D, и угла ∠С
Для начала найдем гипотенузу этого треугольника. По теореме Пифагора, квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов его катетов.
Теперь найдем острые углы этого треугольника. Сделаем это через их синусы. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. Пусть угол B лежит напротив катета b. Тогда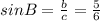
.
Таким образом,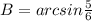
≈ 56,44°.
Зная это, мы можем найти оставшийся угол А.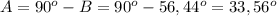
.
В треугольнике напротив большей стороны всегда лежит больший угол. Значит, наше утверждение правильно. Катет b больше катета a. Поэтому угол B - тот, который лежит напротив катета b, угол A - тот, что лежит напротив катета a.