1. Даны точки A(0; - 1), B(- 1;0), C(0;0) и D(0; - 1). Укажите те из них, которые лежат на прямой
3x - 3y -3 = 0.
2. Найти расстояние между точками А (1; -2) и В (-2; 2)
3. Напишите уравнение прямой, проходящей через точки А (2; 3) и В

Показать ответ

Ответ:

kristinasav051

21.09.2021 10:41

108см²

Объяснение:

Фигура квадрат

Формула нахождения периметра квадрата

Р=4*АВ.

Найдем из этой формулы сторону квадрата.

АВ=Р:4=48:4=12 см сторона квадрата.

Теперь найдем площадь квадрата.

Sавсd=AB²=12²=12*12=144см² площадь квадрата.

Квадрат разделен на 4 равных треугольника.

Найдем площадь одного из этих треугольников.

S∆AED=Saвсd:4=144:4=36см² площадь одного треугольника.

Площадь фигуры, которой нам нужно найти состоит из 3 треугольников, если площадь одного треугольника равна 36, то трёх таких треугольников будет.

SABECD=3*S∆AED=3*36=108см²

0,0(0 оценок)

Ответ:

МирославаКарповичь

27.03.2022 07:17

Дано: ΔABC - прямоугольный, ∠C = 90°, ∠ABC = 60°, AC = 6 см.

Найти: а) AB; б) CD

Решение: 1) Рассмотрим ΔABC: ∠ABC = 60°, ∠C = 90°, ∠A = 30° (т. к. 180° - (90° + 60°) = 30); Найдем сторону AB через синус угла ABC (синус острого угла равен отношению противолежащего катета к гипотенузе): sin60° =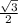 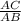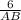$\frac{\sqrt{3}}{2}$ = $\frac{AC}{AB\\}$ = $\frac{6}{AB}$ ; Отсюда AB = 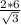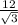$\frac{2*6}{\sqrt{3} }$ = $\frac{12}{\sqrt{3} }$ см.

2) Рассмотрим ΔACD, в котором ∠D = 90°, а ∠CAD = 30° (из 1); Согласно свойству прямоугольного треугольника с углом в 30°, катет, лежащий напротив угла в 30°, равен половине гипотенузы, следовательно, CD = 1/2*AC = 1/2*6 = 3 см.

ответ: а)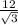 $\frac{12}{\sqrt{3} }\\$ см; б) CD = 3 см.