1. какое число спиц содержит колесо, у которого угол между любыми двумя соседними спицами равен 72 градусов? 2. известно что в прямоугольном треугольнике abc с прямым углом a гипотенуза bc 20 sinc0. 3, определить длину катета ab 3. дуга bd окружности равна 60. радиус равен 9. найдите длину хорды bd.
Опустим перпендикуляр AE из вершины A на прямую CB. Площадь трапеции AECD равна сумме площадей параллелограмма ABCD и треугольника AEB. Опустим перпендикуляр DF из вершины D на прямую CD. Тогда площадь трапеции AECD равна сумме площадей прямоугольника AEFD и треугольника DFC. Прямоугольные треугольники AEB и DFC равны, а значит, имеют равные площади. Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника AEFD, т.е. равна AE • AD. Отрезок AE – высота параллелограмма, соответствующая стороне AD, и, следовательно, S = a • h. Теорема доказана.
Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности и всегда находится внутри треугольника. Пусть OD = 3x и OB = 5x. CD = CE как касательные к окружности; OE = OD = 3x как радиусы, проведенные в точку касания.
По условию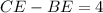
. По т. Пифагора из треугольника BOE
Далее из прямоугольного треугольника BDC по т. Пифагора:
Первый корень не удовлетворяет условию, значит x = 2 см.
Тогда BE = 4x = 8 см, значит CE = BE + 4 = 8 + 4 = 12 см
CD = CE = 12 см, а так как BD является медианой и высотой, то
AC = 2 * CD = 2 * 12 = 24 см; AB = BC = CE + BE = 12 + 8 = 20 см
P = AB + BC + AC = 20 + 20 + 24 = 64 см.