1. На сторонах параллелограмма ABCD (рис. 5.3) отложены равные отрезки AE
CF. Является ли четырехугольник BFDE параллело-
граммом?
D
F
C С
D
C С
F
E
А
В
E
A
В
Рис. 5.3
Рис. 5.4​

По стороне основания правильного треугольника найди радиус вписанной окружности ОК
По ОК и углу МКО найди высоту боковой грани МК
Далее площадь одной боковой грани, а затем и боковую поверхность
Площадь основания=(1/2)a^2sin60°, где а - сторона основания

б)расстояние от вершины основания до противоположной боковой грани.
На чертеже соответствующего отрезка нет
Пусть ВЕ- высота, опущенная из В на МК (докажите, что это перпендикуляр к плоскост МАС)
Находим ее из прямоугольного треугольника ВЕК: угол ВКЕ=45, ВК- медиана в правильном треугольнике со стороной а равна a√3/2

1) Рассмотрим ΔOKN: угол К прямой, а сторона KN равна:

     

     Поскольку пирамида правильная, то в основании лежит квадрат, а значит сторона

     основания (например AD) равна:

     

 

2)  Рассмотрим ΔOKN: угол К прямой, а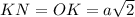

      Это говорит о том, что прямоугольный ΔOKN равнобедренный, и улы при основании

      равны 45⁰. Таким образом, угол между боковой гранью и основанием равен:

      

 

 3) Полная площадь пирамиды равна:

     

 

4)  Рассотянием от центра основания пирамиды до плоскости боковой грани будет

     высота ΔOKN, проведённая к ON (на рисунке отрезок KL).

     ΔNLK~ΔOKN, значит верно соотношение: