1. определите вид треугольника, если два его угла равны: 1) 30 и 40 2) 25 и 65 2. найдите углы прямоугольного треугольника, в котором один из острых углов в два раза больше другого острого угла. 3.найдите углы при основании равнобедренного треугольника, если угол при вершине равен 400. 4. найдите
угол между боковой стороной равнобедренного треугольника и медианой, проведенной к основанию, если угол при основании равнобедренного треугольника равен 500. 5. внешние углы треугольника abc при вершинаха и с равны по 1000. какова величина внешнего угла при вершинев?

1-случай. Если первый угол в вершине 48°, то второй угол 66.°

2-случай. Если первый угол на основании ∠A=∠C=48°, то второй угол 84°.

Объяснение:

Пусть в треугольнике ΔABC равнобедренный. Пусть ∠B - угол в вершине, тогда углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой, то есть углы на основании равны: ∠A=∠C.

1-случай. Пусть ∠B=48°. Сумма внутренних углов треугольник равна 180°=∠A+∠C+∠B, отсюда ∠A+∠C=180°-∠B=180°-48°=132°. Но ∠A=∠C и поэтому ∠A=∠=132°:2=66.°

2-случай. Пусть ∠A=∠C=48°. Тогда ∠B=180°-∠A-∠B=180°-48°-48°= =180°-96°=84°.

В правильной треугольной призме ABCA1B1C1 площадь боковой поверхности в 12 раз больше площади основания. Найдите угол наклона прямой BC1 к плоскости основания. ответ дайте в градусах.

Объяснение: S(бок)=12S(осн)

Т.к призма правильная , то СС₁⊥( АВС) и АВ=ВС=АС .

Углом наклона между прямой BC₁ к плоскости основания является угол между прямой и ее проекцией⇒∠С₁ВС.

Пусть сторона основания а , боковое ребро h. Тогда   S(бок)=Р(осн)*СС₁=3аh ,  S(осн)=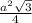

3аh  =12*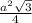    ⇒ h=a√3 .

ΔСВС₁- прямоугольный, tg(∠CBC₁)=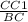  , tg(∠CBC₁)= 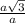, tg(∠CBC₁)=√3  , tg(∠CBC₁)=60°.