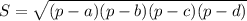1. Основания усеченной пирамиды - прямоугольные прямоугольники со сторонами 2 и 4. Если боковые стенки усеченной пирамиды равны 5, то найдите площадь ее полной поверхности. Начертите)
Проведём также диагональ CA: он проходит через ΔBCD.
ΔBCD — равнобёдренный, так как:
А в свойствах равнобёдренного треугольника входит то, что высота, медиана, и биссектриса, проведённая с вершины к основанию — одно и то же, что и означает, что наш отрезок CO — медиана, и поэтому делит диагональ BD — на 2 равные части.
б)
Я не вижу в этом варианте заданное условие. А если она и вправду есть, то найти площадь, зная то, что отрезки являются "целыми числами", я не смогу.
Но площадь четырёхугольника можно найти — зная всего-лишь его стороны:
Потужність (N, P, W) — робота, що виконана за одиницю часу, або енергія, передана за одиницю часу:
{\displaystyle N={\frac {A}{t}}}{\displaystyle N={\frac {A}{t}}},
де N — потужність, А — виконана робота, t — проміжок часу, за який ця робота виконана.
У системі SI потужність вимірюється у Ватах. Іншою одиницею вимірювання, яка ще й досі широко використовується, є кінська сила (1 к.с. = 735,5 Вт).
Объяснение:
Потужність (N, P, W) — робота, що виконана за одиницю часу, або енергія, передана за одиницю часу:
{\displaystyle N={\frac {A}{t}}}{\displaystyle N={\frac {A}{t}}},
де N — потужність, А — виконана робота, t — проміжок часу, за який ця робота виконана.
У системі SI потужність вимірюється у Ватах. Іншою одиницею вимірювання, яка ще й досі широко використовується, є кінська сила (1 к.с. = 735,5 Вт).
16.
а)
Диагональ BD — делит четырёхугольник на 2 произвольных треугольника: ΔBCD; ΔBAD.
Проведём также диагональ CA: он проходит через ΔBCD.
ΔBCD — равнобёдренный, так как: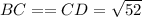
А в свойствах равнобёдренного треугольника входит то, что высота, медиана, и биссектриса, проведённая с вершины к основанию — одно и то же, что и означает, что наш отрезок CO — медиана, и поэтому делит диагональ BD — на 2 равные части.
б)
Я не вижу в этом варианте заданное условие. А если она и вправду есть, то найти площадь, зная то, что отрезки являются "целыми числами", я не смогу.
Но площадь четырёхугольника можно найти — зная всего-лишь его стороны: