1.Плоскость α пересекает стороны АВ и ВС треугольника АВС в точках D и Е соответственно, причем АС параллельна плоскости α.
Найдите АС, если ВD: АD= 4:5, DЕ=16 см. (4б)
2.Какое наибольшее количество прямых можно провести через различные
пары из четырех точек пространства? Выполнить рисунок. (2б)
3 Начертите прямоугольный параллелепипед. Запишите по две пары:
а) параллельных ребер; б) скрещивающихся ребер;
в) пересекающихся ребер. (3б)
4.Сколько плоскостей можно провести через различные пары из четырех
параллельных прямых, никакие три из которых не лежат в одной плоскости?
Сделать чертеж. (2б)
Сумма противолежащих углов вписанного четырехугольника равна 180°. Четырехугольник АВСD - вписанный, ⇒ ∠ВАD+∠BСD=180°. Угол ВАL - развернутый. Сумма смежных углов равна 180°. ⇒ ∠BАD +∠LAD =180°. На приложенном рисунке ∠ LAD обозначен как 1, а ∠KCD – 2. Следовательно, угол С =∠1.
Рассмотрим треугольники АLD и СКD. Вертикальные углы при D равны – Вычтя их из суммы углов треугольника, получим <1+<L=<2+<K. По условию <K-< L=60°. ⇒ ∠К=60°+<L Заменим в предыдущем уравнении угол К найденным значением: ∠1+∠L=<2+60°+∠L, откуда ∠1=∠2+60°. Равный углу 1 ∠С=∠2+60° , ⇒ ∠2=∠С-60°, поэтому ∠С-60°+∠С=180°, ⇒ 2С=240°, ∠С=120° и, следовательно, угол ВАD=60°
Задание 1
ответ: Да, существует. Это правильный 8-ми угольник (см. картинку №1).
Объяснение:
Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:
S = 180°(n-2)
Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒
S = 135° × n
Отсюда выходит что:
135n = 180(n-2)
Находим n:
135n = 180n - 360
180n - 135n = 360
45n = 360
n = 360 ÷ 45
n = 8 (количество сторон правильного многоугольника)
Задание 2
ответ: Количество сторон правильного многоугольника = 12 (см. картинку №2).
Объяснение:
Пускай внутренний угол правильного многоугольника = x°
⇒ смежный с ним угол = 0,2x°
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол = 180°.
⇒ x + 0,2x = 180
1,2x = 180
x = 180 ÷ 1,2
x = 150° (внутренний угол выпуклого многоугольника)
Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:
S = 180°(n-2)
Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒
S = 150° × n
Отсюда выходит что:
150n = 180(n-2)
Находим n:
150n = 180n - 360
180n - 150n = 360
30n = 360
n = 360 ÷ 30
n = 12 (количество сторон правильного многоугольника)
Задание 3
а) ответ: Площадь многоугольника = 64 см².
Объяснение:
Правильный многоугольник, в котором n = 4 это КВАДРАТ.
Диаметр окружности d = 2r, где r - радиус
Известно что сторона квадрата a равна диаметру d вписанной в него окружности
⇒ d = a = 2r = 2×4 = 8 cm.
Площадь квадрата = a² = 8² = 64 cm²
б) ответ: Радиус вписанной окружности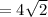
см.
Объяснение:
Известно что сторона квадрата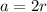
, где r - радиус вписанной окружности.
Так же известно что сторона квадрата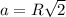
, где R - радиус описанной окружности ⇒
в) ответ: Периметр многоугольника = 16 см.
Объяснение:
Известно что сторона квадрата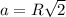
, где R - радиус описанной окружности
⇒
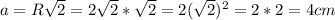
Периметр любого многоугольника P = n·a, где a - сторона многоугольника, n - количество его сторон.
⇒ P = 4 × 4 = 16 cm