1.Радіус кола дорівнює 7см.Чому дорівнює діаметр цього кола.
А.3,5см, Б.7см, В.14см,Г.10см
2.OB радіус кола,AC-його діаметр.Чому дорівнює кут COB,якщо кут OBA =40°
3.Діаметр кола дорівнює 18см.На відстані а см від його центра проведено пряму AB.При якому з наведених значень а пряма AB і подане коло мають дві спільні точки?
4.Чому дорівнює радіус кола,вписаного в прямокутний трикутник зі сторонами 10см,24см,26см?
5.Точка дотику вписаного кола ділить бічну сторону рівнобедреного трикутника на відрізки 4см і 6см починаючи від основи.Знайдіть периметр трикутника.
6.Хто з учнів сформулював неправельне твердження ?
А.через точку позначенну на колі можна провести тільки один радіус .
Б.Центр кола описаного навколо прямокутного трикутник-це вершина прямого кута.
В.Якщо хорди розміщенні на однаковій відстані від цетра кола то вони рівні.
Г.Через точку,щолежить поза колом,можна провести дві дотичних до цього кола.
1)
Если трапеция равнобедренная, то АБ=СД=5, следовательно АБ+СД=10.
Тогда сумма двух оснований равна 32-10=22.
Площадь равна средняя линия * h(высоту)
Ср линия = 22/2=11.
Из формулы площади найдем высоту:
h=S/ср.лин
следовательно высота равна 44/11=4
ответ: h=4
2)
S(трапецииABCD) = (AD + BC) : 2 * h
h - высота трапеции и треугольника ACD
S(ACD) = 1/2 * AD * h, следовательно
h = S(ACD) / (1/2 * AD) = 30 / (1/2 * 10) = 30 : 5 = 6 см
S(трапецииABCD) = 1/2*(10 + 8) * 6 = 9 * 6 = 54 см²
P.S. 1/2 -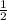
/ - дробь
0,2
Объяснение:
ΔOAB - прямоугольный, <BOA = 45°, ⇒ <ABO = 90° - 45° = 45°, ⇒ ΔOAB - равнобедренный, ⇒ OA = OB.
Пусть AB = x, тогда AD = x = CD, т.к. ABCD - квадрат.
Построим отрезок OC, OC - радиус по построению, т.к. О - центр окружности, а точка C лежит на окружности, ⇒ OC = 1.
Рассмотрим прямоугольный ΔODC: OD = OA + AD = x + x = 2x, CD = x, тогда по теореме Пифагора OC² = OD² + CD² , получаем уравнение:
1² = (2x)² + x²
1 = 4x² + x²
5x² = 1
x² = 1/5 = 0,2