#1 Сторони трикутника відносять як 2 : 3 : 3. Знайдіть найменшу його сторону, якщо периметр трикутника, утвореного середніми лініями даного трикутника дорівнює 80 см.
#2
Середня лінія рівнобедреного трикутника проведена між бічною стороною і основою дорівнює 5 см, а основа трикутника на 3,5 см більша за середню лінію. Знайдіть периметр трикутника.
46.5. Искомая площадь вычисляется:
S=S₁-S₂-S₃,
S₁=π(AB)²/8; S₂=π(AD)²/8; S₃=π(DB)²/8.
S=π/8(AB²-AD²-DB²).
Подставим AB=AD+DB, CD²=AD*DB.
S=π/8(AD²+DB²+2AD*DB-AD²-DB²)=π*AD*DB/4 = π*CD²/4.
46.4. Рассмотрим четверть квадрата (Рис. ниже) со стороной a. Найдем S₁.
S₁=Sсек -Sтреуг, где Sсек - площадь сектора круга, ограниченного радиусами AB и AC, Sтреуг - площадь треугольника ABC.
Sсек = Sкр/4 = πa²/16.
Sтреуг = a²/8.
S₁ = a²/8*(π/2-1).
Искомая площадь: S=8*S₁ = a²*(π/2-1). По условию a=4 см.
S = 16(π/2-1) см.
46.6. Площадь (из задачи 46.5) вычисляется:
S=π*CD²/4 = π*AD*DB/4 = π*6*4/4 = 6π см².
Длина дуги окружности диаметра AB: L₁=πAB/2=5π см.
Длина дуги окружности диаметра AD: L₂=πAD/2=3π см.
Длина дуги окружности диаметра DB: L=πDB/2=2π см.
Периметр: L=L₁+L₂+L₃ = 5π+3π+2π = 10π см.
Дано: ΔABC - прямоугольный, ∠C = 90°, ∠ABC = 60°, AC = 6 см.
Найти: а) AB; б) CD
Решение: 1) Рассмотрим ΔABC: ∠ABC = 60°, ∠C = 90°, ∠A = 30° (т. к. 180° - (90° + 60°) = 30); Найдем сторону AB через синус угла ABC (синус острого угла равен отношению противолежащего катета к гипотенузе): sin60° =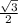
= 
= 
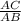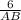; Отсюда AB = 
= 
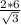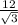см.
2) Рассмотрим ΔACD, в котором ∠D = 90°, а ∠CAD = 30° (из 1); Согласно свойству прямоугольного треугольника с углом в 30°, катет, лежащий напротив угла в 30°, равен половине гипотенузы, следовательно, CD = 1/2*AC = 1/2*6 = 3 см.
ответ: а)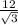
см; б) CD = 3 см.