1.Точка Т – середина отрезка МР. Найдите координаты точки Р, если
Т (-3;4) и М (-5; -7).
2. а) АВ – диаметр окружности с центром О. Найдите координаты центра окружности, если А (7; -2) и В (-1;-4). [2]
В)Запишите уравнение окружности, используя условия пункта а. [2]
3. Дано: , . Напишите уравнение медианы АМ. [3]
4.Точки А(-4;-3), В(-4;5), С(2;5), D(8;-3) – вершины прямоугольной трапеции с основаниями ВC и АD. Найдите длину средней линии [3]
ответ: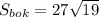
Объяснение: РАВС - правильная треугольная пирамида, АВ=12 , РН=8, А₁В₁С₁║АВС .
АСВ – правильный треугольник, Н – центр данного треугольника (центр вписанной и описанной окружностей). РМ – апофема заданной пирамиды. ММ₁ – апофема усеченной пирамиды. Согласно свойству параллельных плоскостей (две параллельные плоскости пересекают любую третью плоскость так, что линии пересечения параллельны), имеем несколько пар подобных треугольников с равным коэффициентом подобия. В частности
Найдём НМ - радиус вписанной окружности в правильный треугольник:
Рассм. ΔРНМ: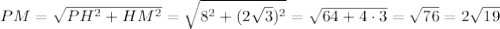
а)8+2а
б)а и (180°-а)°
в) Р=22, углы 60° и 120°
Объяснение:
а) Так как у ∆ АВН катет напротив угла 30° равен 2 то гипотенуза ( в два раза больше) равна 4. Периметр равен 2 (ВС+АВ) ( по определению противоположные стороны равны)
б)Так как у ∆ЕКР высота является медианой он равнобедренный (свойство) тогда угол КРЕ = углу КЕР= углу М = а (свойство параллелограмма) и односторонний ему равен (180°- а)
в)∆QRN — равносторонний так как ST=QR(по определению параллелограмма)=4 ( что равно QN) тогда угол Q = 60° = углу S и односторонний ему угол Т = 180°-60°=120°