1. Знайдіть гіпотенузу АВ прямокутного трикутника АВС (ÐС=90), якщо АС=3см, cosÐA = 0.25.

А) 12 см; Б) 0,75 см; В) 1,75 см; Г) 0,12 см

2. Знайдіть гіпотенузу АВ прямокутного трикутника АВС (ÐC=90), якщо ВС=5см, sinÐA=⅔.

А) 75 см; Б) 15 см; В) 7,5 см; Г) 21 см

3. Обчисліть значення виразу: tg45° +sin30°

А) ½ ; Б) 1½ ; В) 2; Г) ¼

4. Основа рівнобедреного трикутника має довжину 10 см, а його бічна сторона - 13см. Знайдіть тангенс кута при основі трикутника.

А)2,4; Б) 2 ; В)⅚ ; Г)¾

5. У рівнобічній трапеції АВСД відомо, що АВ=СД=2см, ВС=6см, АД=8см. Знайдіть ÐА та ÐВ.

А)60°, 120° Б) 45°, 135° В) 30°, 150° Г) 20°, 160°

Показать ответ

Ответ:

vanyadrachuk2004

28.09.2020 14:45

Если сделать рисунок, то будет видно, что точка B лежит в пслокости OXZ, так как ордината точки B равна нулю. Рассмотрим треугольник ABO. Он прямоугольный, одна сторона его OA лежит на оси ординат. Из условия задачи угол ABO=30 градусов (это как раз угол пересечения прямой AB с осью OXZ). Найдем длину OA.

OA=OB*tgABO=OB*tg30

Чтобы найти OA, найдем чему равно OB.

Для этого опустим перпендикуляры из точки B на ось x (пересечение - точка K) и ось z (пересечение - точка L). Из координат точки B понятно, что BK=1, BL=1

Из теоремы Пифагора находим, что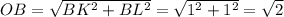 $OB=\sqrt{BK^2+BL^2}=\sqrt{1^2+1^2}=\sqrt{2}$

Теперь находим OA:

$OA=OB*tg30=\sqrt{2}*\frac{\sqrt{3}}{3}=\frac{\sqrt{6}}{3}$

OA - это и есть значение ординаты точки A

Так как A лежит на оси ординат, ее координаты x=0 и z=0

Возможны два случая:

1) A лежит в положительной части оси ординат

Тогда координаты точки будут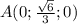 $A(0;\frac{\sqrt{6}}{3};0)$

2) A лежит в отрицательной части оси ординат

Тогда координаты точки будут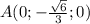 $A(0;-\frac{\sqrt{6}}{3};0)$

0,0(0 оценок)

Ответ:

ТамараБерезанка

22.04.2023 23:56

Т.к. призма прямая, её грани перпендикулярны основаниям.

Грань SA1B1 пирамиды лежит в плоскости АВВ1А1, высота SH перпендикулярна основанию А1В1С1 и параллельна боковому ребру призмы, следовательно, её длина равна длине ребра АА1.

Пусть АВСD - верхнее основание куба, а нижнее A1B1C1D1.

Диагонали основания пирамиды OA1B1C1D1 совпадают с диагоналями квадрата А1В1С1D1, высота ОН равна расстоянию между параллельными основаниями куба, т.е. длине его ребер - 8 дм.

Диагональное сечение пирамиды - треугольник А1ОС1. Основание А1С1 - диагональ квадрата со стороной А1В1=8. А1С1=8√2 (как диагональ квадрата).

S(A1OC1)=OH•A1C1:2=8•8√2*2=32√2 дм²

В этой задаче допущена неточность. Длины ребер правильной шестиугольной призмы равны.

В основании этой призмы правильный шестиугольник, а все 6 граней - квадраты. Площадь каждого 96:6=16 см²

Тогда ребро призмы √16=4 см.

Правильный шестиугольник можно разделить на 6 правильных треугольников, и длина бóльшей его диагонали равна длине 2-х ребер.

На рисунке приложения АD и А1D1 - бóльшие диагонали оснований, а А1D - бóльшая диагональ призмы.

По т.Пифагора

А1D=√(AA1²+AD²)=√(4²+8²)=4√5