17. Наибольшее и наименьшее расстояния от данной точки, лежа- щей вне окружности, до точек окружности равны соответствен- но 50 см и 30 см. Найдите радиус данной окружности: А. 10 см. В. 20 см. С. 30 см. D.40см
5) Сумма смежных углов равна 180°. х - один угол, 2х - другой угол. х + 2х = 180 3х = 480 х = 180 : 3 х = 60° - первый угол. 60° · 2 = 120° - второй угол. ответ: 60° и 120°.
В правильной треугольной призме ABCA1B1C1 площадь боковой поверхности в 12 раз больше площади основания. Найдите угол наклона прямой BC1 к плоскости основания. ответ дайте в градусах.
Объяснение: S(бок)=12S(осн)
Т.к призма правильная , то СС₁⊥( АВС) и АВ=ВС=АС .
Углом наклона между прямой BC₁ к плоскости основания является угол между прямой и ее проекцией⇒∠С₁ВС.
Пусть сторона основания а , боковое ребро h. Тогда S(бок)=Р(осн)*СС₁=3аh , S(осн)=
138° : 2 = 69°
ответ: 69°.
2) 180° : (2 + 3 + 4) = 20° - 1 часть.
2 х 20° = 40°
3 х 20° = 60°
4 х 20 = 80°
ответ: 40°, 60°, 80°.
3) АВ = АС + ВС
ВС = АВ - АС = 17 - 9 = 8 (см)
ответ: ВС = 8 см.
4) 180° : (8 + 5 + 2) = 12° - 1 часть.
8 х 12° = 96°
5 х 12° = 60°
2 х 12° = 24°
180° - 96° = 84°
180° - 60° = 120°
180° - 24° = 156°
ответ: 84°, 120°, 156° - внешние углы треугольника.
5) Сумма смежных углов равна 180°.
х - один угол,
2х - другой угол.
х + 2х = 180
3х = 480
х = 180 : 3
х = 60° - первый угол.
60° · 2 = 120° - второй угол.
ответ: 60° и 120°.
6) 54 : (2 + 7) = 6 (см) - одна часть.
2 · 6 = 12 (см) - АК.
7 · 6 = 42 (см) - ВК.
В правильной треугольной призме ABCA1B1C1 площадь боковой поверхности в 12 раз больше площади основания. Найдите угол наклона прямой BC1 к плоскости основания. ответ дайте в градусах.
Объяснение: S(бок)=12S(осн)
Т.к призма правильная , то СС₁⊥( АВС) и АВ=ВС=АС .
Углом наклона между прямой BC₁ к плоскости основания является угол между прямой и ее проекцией⇒∠С₁ВС.
Пусть сторона основания а , боковое ребро h. Тогда S(бок)=Р(осн)*СС₁=3аh , S(осн)=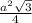
3аh =12*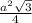
⇒ h=a√3 .
ΔСВС₁- прямоугольный, tg(∠CBC₁)=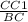
, tg(∠CBC₁)= 
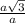, tg(∠CBC₁)=√3 , tg(∠CBC₁)=60°.