я бы пошёл таким путём: очевидно, что треугольник МАС прямоугольный, причём катеты у него 5 и 12 откуда мы можем найти угол МСА (по теореме синусов, хотя бы) теперь рассмотрим треугольник ЕОС (О - центр окружности) он равнобедренный со сторонами ОЕ и ОС по 6 можем найти его углы ЕСО = МСА СЕО = ЕСО = МСА ЕОС = 180 - 2*МСА теперь рассмотрим треугольник ЕОА он тоже равнобедренный со сторонами ЕО и АО по 6 и угол ЕОА = 180 - ЕОС = 180 - 180 - (-2*МСА) = 2*МСА теперь мы знаем две стороны (по 6) и угол между ними (ЕОА = 2*МСА) по теореме косинусов можем найти противоположную сторону АЕ всё
очевидно, что треугольник МАС прямоугольный, причём катеты у него 5 и 12
откуда мы можем найти угол МСА (по теореме синусов, хотя бы)
теперь рассмотрим треугольник ЕОС (О - центр окружности)
он равнобедренный со сторонами ОЕ и ОС по 6
можем найти его углы
ЕСО = МСА
СЕО = ЕСО = МСА
ЕОС = 180 - 2*МСА
теперь рассмотрим треугольник ЕОА
он тоже равнобедренный со сторонами ЕО и АО по 6
и угол ЕОА = 180 - ЕОС = 180 - 180 - (-2*МСА) = 2*МСА
теперь мы знаем две стороны (по 6) и угол между ними (ЕОА = 2*МСА)
по теореме косинусов можем найти противоположную сторону АЕ
всё
a = 5 см,
b = 4 см,
c = 7 см.
Найти R.
Запишем теорему синусов:
числитель и знаменатель дроби слева последнего равенства домножим на (b·c).
С учётом того, что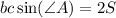
, где S - площадь данного в условии треугольника, имеем
Площадь треугольника можно найти по формуле Герона:
Найдем, сначала, площадь треугольника.
p = (5+4+7)/2 = (9+7)/2 = 16/2 = 8 см.
S = √(8·(8-5)·(8-4)·(8-7)) = √(8·3·4·1) = 4·(√6) см²
Теперь найдем радиус описанной окружности.
R = 5·4·7/(4·4·(√6)) = 5·7/(4·(√6)) = 35·(√6)/(4·6) = 35·(√6)/24 см.
Теперь найдём длину окружности, описанной около данного треугольника.
L = 2πR = 2π·35·(√6)/24 см = π·35·(√6)/12 см.