1. площа прям. трик.= 1/2 катет*катет.(один катет=12 за умовою, другий - невідомий). 2. З вершини прямого кута опустимо пкрпендикуляр на гіпотенузу. за теоремою Піфагора знайдемо довжину перпендикуляра як невідомого катета: під коренем 144-64= під кор. 80= під кор. 16*5=4*корінь з пяти. 3. у 8 класі вчили, що квадрат цього перпендикуляра, що ми провели = добутку двох проекцій, одна 8 за умовою задачі, а другу позначимо х. тому 8х=(4*корінь з пяти) у квадраті 8х=80 х=10 - це друга проекція. отже, вся гіпотенуза=10+8=18. 4. за т.Піфагора знайдем невідомий другий катет. під коренем 18 у квадраті-12 у квадраті=6*корінь з пяти. 5. площа=1/2 *12*6корінь5=36*корінь з пяти.
1) Через пересекающиеся прямые можно провести плоскость. ⇒ а и b лежат в одной плоскости. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. А1В1||А2В2.
∆ А1КВ1~А2КВ2, т.к. углы при пересечении параллельных оснований секущими а и b равны, и угол К - общий.
Из подобия следует: КВ1:КВ2=А1В1:А2В2=3/4
Примем В1В2=х, тогда КВ2=14+х
14:(14+х)=3:4
56=42+3х ⇒ ⇒
см
2) Медианы треугольника пересекаются, параллельны плоскости альфа, следовательно, плоскость треугольника, в которой они лежат, параллельна плоскости альфа.
СЕ и ВF параллельны ( дано), следовательно, через них можно провести плоскость, притом только одну.
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.⇒ СВ||EF.
Четырехугольник, у которого противоположные стороны попарно параллельны, является параллелограммом, ч.т.д.
3) Все грани параллелепипеда ABCDA1B1C1D1 - квадраты со стороной a.⇒ этот параллелепипед - куб.
DA1В1С - прямоугольник, т.к. по т. о 3-х перпендикулярах диагонали А1D и В1С параллельных граней перпендикулярны ребрам А1В1 и DC . Проведем через середины АD и ВC прямые КМ и ОН параллельно А1D и В1C, соединим К и О, М и Н. Пересекающиеся КО и КА параллельны пересекающимся АА1 и АD. ⇒
Плоскость сечения МКОН параллельна плоскости DA1B1C ⇒ . Стороны сечения КМНО пересекают ребра АА1, ВВ1, ВС и AD в их середине. КМНО - прямоугольник.
В параллельных гранях диагонали А1D=B1C=a:sin45°=a√2
КМ и ОН –– средние линии ∆ АА1D и ВВ1С соответственно и равны половине А1D- равны
2. З вершини прямого кута опустимо пкрпендикуляр на гіпотенузу. за теоремою Піфагора знайдемо довжину перпендикуляра як невідомого катета: під коренем 144-64= під кор. 80= під кор. 16*5=4*корінь з пяти.
3. у 8 класі вчили, що квадрат цього перпендикуляра, що ми провели = добутку двох проекцій, одна 8 за умовою задачі, а другу позначимо х. тому 8х=(4*корінь з пяти) у квадраті
8х=80
х=10 - це друга проекція. отже, вся гіпотенуза=10+8=18.
4. за т.Піфагора знайдем невідомий другий катет. під коренем 18 у квадраті-12 у квадраті=6*корінь з пяти.
5. площа=1/2 *12*6корінь5=36*корінь з пяти.
1) Через пересекающиеся прямые можно провести плоскость. ⇒ а и b лежат в одной плоскости. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. А1В1||А2В2.
∆ А1КВ1~А2КВ2, т.к. углы при пересечении параллельных оснований секущими а и b равны, и угол К - общий.
Из подобия следует: КВ1:КВ2=А1В1:А2В2=3/4
Примем В1В2=х, тогда КВ2=14+х
14:(14+х)=3:4
56=42+3х ⇒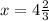 ⇒
⇒
2) Медианы треугольника пересекаются, параллельны плоскости альфа, следовательно, плоскость треугольника, в которой они лежат, параллельна плоскости альфа.
СЕ и ВF параллельны ( дано), следовательно, через них можно провести плоскость, притом только одну.
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.⇒ СВ||EF.
Четырехугольник, у которого противоположные стороны попарно параллельны, является параллелограммом, ч.т.д.
3) Все грани параллелепипеда ABCDA1B1C1D1 - квадраты со стороной a.⇒ этот параллелепипед - куб.
DA1В1С - прямоугольник, т.к. по т. о 3-х перпендикулярах диагонали А1D и В1С параллельных граней перпендикулярны ребрам А1В1 и DC . Проведем через середины АD и ВC прямые КМ и ОН параллельно А1D и В1C, соединим К и О, М и Н. Пересекающиеся КО и КА параллельны пересекающимся АА1 и АD. ⇒
Плоскость сечения МКОН параллельна плоскости DA1B1C ⇒ . Стороны сечения КМНО пересекают ребра АА1, ВВ1, ВС и AD в их середине. КМНО - прямоугольник.
В параллельных гранях диагонали А1D=B1C=a:sin45°=a√2
КМ и ОН –– средние линии ∆ АА1D и ВВ1С соответственно и равны половине А1D- равны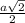
КО=МН=АВ=а
Р (КМНО=2(МН+КМ)=2a+2•(a√2/2)=a•(2+√2)