2) Промінь ск ділить кут АСВ на два кути, причому кут Аск на 30° більний ва кут КСВ. Знайдіть кут між бісектрисою кута АСві променем ск, якщо кут АСВ дорівнює 100°.
В треугольнике ABC AC= BC, K - точка пересечения биссектрис треугольника, а O - точка, равноудаленная от всех вершин треугольника. Отрезок OK пересекает сторону AB в точке E и точкой пересечения делится пополам. Найдите углы треугольника ABC.
------
Точка К равноудалена от сторон треугольника, поэтому является центром вписанной окружности.
Точка О - равноудалена от вершин треугольника и является центром описанной окружности. Точка К лежит на высоте и медиане к АВ ( на срединном перпендикуляре), точка О лежит на срединном перпендикуляре к АВ, поэтому С, К, Е и О принадлежат одной прямой СО.
Т.к. отрезок КО пересекает АВ, точка О расположена вне треугольника.
Высота и медиана СЕ ⊥ АВ и делит его пополам.
Соединим точки К и О с вершинами А и В.
В получившемся четырехугольнике АКВО отрезки АЕ=ВЕ, КЕ=ОЕ.
Треугольники, на которые КО и АВ делят этот четырехугольник, прямоугольные и равны по двум катетам.
Следовательно, АК=ВК=ВО=АО, и АКВО - ромб. АВ - его диагональ и делит его углы пополам.
Пусть ∠ЕАО=α, тогда ∠КАЕ=α, а, так как АК - биссектриса угла САВ, то ∠САК=∠ЕАК, и ∠САЕ=2α.
∆СОА - равнобедренный ( по условию ОА=ОС=ОВ).
∠ОСА=∠ОАС=3α.
Сумма острых углов прямоугольного треугольника равна 90°.
1) 6 см4 2) 18 см; 3)MN=12 (см); 4.12√3(см); 5. ∠1=30°, ∠2= 60°, катет= 12√3 см; 6. 64/√3≈37.6 cм; 7. 20/√3≈11,5 см 8. 4 см і 4√3 см.
Пояснення: с- гіпотенуза, а і b- катети
1.Інший кут(протилежний до заданого)катета=180°-(90°+30°)=60° за теоремою синусів прилеглий катет а =12*sin 60°=12*√3/2=6 √3(см)
2. коли кут = 45°, то інший кут теж рівен 45°- трикутник рівнобедрений,
с²=2а².(см)
3. за теоремою синусів : /*2
MN=12 (см)
4. як у першій задачі катет=24*sin 60°=24*√3/2=12√3(см)
5. якщо у прямокутному Δ, катет= 1/2 гіпотенузи, то це катет, що лежить проти кута в 30°.
відповідь: ∠1=30°, ∠2= 60°, катет= 12√3 см.
6. За властивостями ромба : його діагоналі є бісектрисами кутів, у точці перетину ділять себе навпіл, та є перпендикулярні одна до другої. Так як один з кутів 120°, то поділений діагоналю навпіл= 120°:2=60°., трикутник утворений цією діагоналлю буде рівностороннім, так як протилежні кути в ромбу рівні, а сума усіх кутів Δ=60°. Друга напівдіогональбуде висотою цього трикутника( бо діагоналі утворюють між собою прямий кут) Знайдемо сторону ромбу , с²=8²+(с/2)²
4с²-с²=64*4; 3с²=256.
P=4*16/√3=64/√3≈37.6 cм
7. за теоремою Піфагору знайдемо сторону в утвореному висотою прямокутному трикутнику с²=10²+ (с/2)²;3с²=400. с= √( 400/3)=20/√3≈11,5 см
8. Діагоналі ромба ділять його на 4-ри прямокутних трикутники, які попарно рівні. Так як діагоналі ромба є його бісектрисами,то утворені трикутники мають кути 30°,60°,90°. тоді менша гіпотинуза = 2*2= 4см, а більша 2√3*2=4√3 см
В треугольнике ABC AC= BC, K - точка пересечения биссектрис треугольника, а O - точка, равноудаленная от всех вершин треугольника. Отрезок OK пересекает сторону AB в точке E и точкой пересечения делится пополам. Найдите углы треугольника ABC.
------
Точка К равноудалена от сторон треугольника, поэтому является центром вписанной окружности.
Точка О - равноудалена от вершин треугольника и является центром описанной окружности. Точка К лежит на высоте и медиане к АВ ( на срединном перпендикуляре), точка О лежит на срединном перпендикуляре к АВ, поэтому С, К, Е и О принадлежат одной прямой СО.
Т.к. отрезок КО пересекает АВ, точка О расположена вне треугольника.
Высота и медиана СЕ ⊥ АВ и делит его пополам.
Соединим точки К и О с вершинами А и В.
В получившемся четырехугольнике АКВО отрезки АЕ=ВЕ, КЕ=ОЕ.
Треугольники, на которые КО и АВ делят этот четырехугольник, прямоугольные и равны по двум катетам.
Следовательно, АК=ВК=ВО=АО, и АКВО - ромб. АВ - его диагональ и делит его углы пополам.
Пусть ∠ЕАО=α, тогда ∠КАЕ=α, а, так как АК - биссектриса угла САВ, то ∠САК=∠ЕАК, и ∠САЕ=2α.
∆СОА - равнобедренный ( по условию ОА=ОС=ОВ).
∠ОСА=∠ОАС=3α.
Сумма острых углов прямоугольного треугольника равна 90°.
В ∆ СЕА ∠САЕ+∠АСЕ=5α.
5α=90°, откуда α=90°:5=18°
∠САВ=∠СВА=2•18°=36°
∠АСВ=180°-2•36°=108°.
Відповідь:
1) 6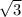
см4 2) 18
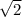см; 3)MN=12
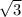(см); 4.12√3(см); 5. ∠1=30°, ∠2= 60°, катет= 12√3 см; 6. 64/√3≈37.6 cм; 7. 20/√3≈11,5 см 8. 4 см і 4√3 см.
Пояснення: с- гіпотенуза, а і b- катети
1.Інший кут(протилежний до заданого)катета=180°-(90°+30°)=60° за теоремою синусів прилеглий катет а =12*sin 60°=12*√3/2=6 √3(см)
2. коли кут = 45°, то інший кут теж рівен 45°- трикутник рівнобедрений,
с²=2а².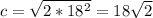
(см)
3. за теоремою синусів :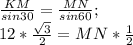
/*2
MN=12
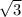(см)
4. як у першій задачі катет=24*sin 60°=24*√3/2=12√3(см)
5. якщо у прямокутному Δ, катет= 1/2 гіпотенузи, то це катет, що лежить проти кута в 30°.
відповідь: ∠1=30°, ∠2= 60°, катет= 12√3 см.
6. За властивостями ромба : його діагоналі є бісектрисами кутів, у точці перетину ділять себе навпіл, та є перпендикулярні одна до другої. Так як один з кутів 120°, то поділений діагоналю навпіл= 120°:2=60°., трикутник утворений цією діагоналлю буде рівностороннім, так як протилежні кути в ромбу рівні, а сума усіх кутів Δ=60°. Друга напівдіогональбуде висотою цього трикутника( бо діагоналі утворюють між собою прямий кут) Знайдемо сторону ромбу , с²=8²+(с/2)²
4с²-с²=64*4; 3с²=256.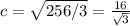
P=4*16/√3=64/√3≈37.6 cм
7. за теоремою Піфагору знайдемо сторону в утвореному висотою прямокутному трикутнику с²=10²+ (с/2)²;3с²=400. с= √( 400/3)=20/√3≈11,5 см
8. Діагоналі ромба ділять його на 4-ри прямокутних трикутники, які попарно рівні. Так як діагоналі ромба є його бісектрисами,то утворені трикутники мають кути 30°,60°,90°. тоді менша гіпотинуза = 2*2= 4см, а більша 2√3*2=4√3 см