Дан параллелограмм ABCD с длинами сторон 12 и 8. Биссектрисы его углов при пересечении образуют четырехугольник. Чему равна длина диагоналей этого четырехугольника?
По свойству параллельных прямых и секущей сумма углов при одной стороне параллелограмма равна 180°. Следовательно, биссектрисы его соседних углов пересекаются под прямым углом. Поэтому четырехугольник, образованный четырьмя биссектрисами параллелограмма - прямоугольник. Обозначим его вершины К, L, M и N.
Биссектрисы параллелограмма, являясь секущими, отсекают от него равнобедренные треугольники ( они делят углы пополам, и накрестлежащие углы тоже равны). Противоположные стороны параллелограмма равны =>
АВ=BQ=AT=CD=CR=DS=8 Тогда ВR=12-CR=4. Аналогично длина отрезков QC,, DT,, AS равна 4.
Отрезки QR и TS равны 12-2•4=4.
По 1-му признаку равенства треугольников ∆ АВТ=∆ RCD и ∆ ABQ=∆ СDS ⇒ их стороны и углы, заключённые между ними, равны.
В равнобедренном треугольнике биссектриса=высота=медиана. ⇒ BL=LT=RN=ND
Биссектрисы противоположных углов параллелограмма параллельны: ВТ║RD, а BR║TD как лежащие на параллельных сторонах ABCD.
1) Ну чертить тебе придётся самому. там не сложно. Сначала окружность, потом внутри неё чертишь произвольный четырёхугольник. Даже с разными длинами сторон, по условию не указано, что правильный. Потом пятиугольник
2) Площадь прямоугольника (обозначается буквой S) равняется произведению двух сторон, имеющих общий угол. То бишь нижнюю или верхнюю умножь на боковую. То бишь S=5*8=40 (см2)
3) Площадь параллелограмма равна длине основания умноженной на высоту. S=6*9=54 (см2)
4) Это можно нагуглить за 10 секунд. Не спрашивай откуда узнал) 900 градусов.
5) Площадь треугольника равняется высоте умноженной на сторону, к которой она проведена. Т.к площадь равна 36, а сторона 6, то высота равна 36/6=6 (см)
6) Площадь трапеции равняется сумме оснований (верхняя и нижняя сторона) поделённой на два, после чего умноженной на высоту.
Значит сторона (обозначим её АВ) равна: АВ= (см)
0.5 тут играет роль деления на два, т.к умножение на 0.5, она же это то же самое, что деление на 2.
7) 1)Находим площадь исходного прямоугольника по формуле из второй задачи (перемножь две стороны, чтобы не умножать число на десятичную дробь переведи дециметры в сантиметры, для этого нужно умножить на 10, т.к 1 дм=10 см. Получится 40 и 32 см).
2)Потом находим площадь одного такого квадрата, умножив 0.2 на 0.2, т.к у квадрата стороны равны. Тут та же история, переводи в сантиметры.
3) делим площадь всего прямоугольника на площадь квадрата и получаем количество квадратов.
4) ???
5) Профит. Попробуй посчитать сам, у тебя получится.
8) Тут уже поинтереснее. Делай рисунок.
Площадь ромба можно двумя перемножив основание на высоту, либо перемножив две диагонали друг на друга, после чего разделив полученное число на два. Пойдём по второму
У ромба все стороны равны, т.е все четыре равны 15 см. А вот диагонали разные. Одна у нас есть и равна 24 см. Диагонали ромба пересекаются под прямым углом, а это значит, что у нас есть прямоугольный треугольник в котором мы знаем 2 стороны. По теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы) найдём половинку второй диагонали. Тут нужен рисунок, но заливать картинку мне лень, извини)
Поэтому объясню на словах, а там тащи сам. Запоминай: в прямоуг. треугольнике катетами называются стороны, которые расходятся из прямого угла, то бишь если сторона в таком треугольнике соприкасается с прямым углом, то это катет. Гипотенуза не соприкасается с прямым углом. В нашем случае (ты увидишь это, когда нарисуешь ромб с диагоналями) под прямым углом по свойству ромба пересекаются его диагонали. Значит, чтобы найти половинку второй диагонали мы рассмотрим треугольник, у которого 2 стороны - это половинки диагоналей, а вторая - любая сторона ромба. Ромб состоит из 4 таких треугольников.
По т. Пифагора сумма квадратов катетов (половинки диагоналей) равна квадрату гипотенузы (сторона ромба), значит:
Половинка диагонали в квадрате равна квадрат гипотенузы минус квадрат известного катета. Полученное значение ставим под корень и находим половинку диагонали уже НЕ в квадрате:
Выглядеть это будет как-то так (буквы сам поставишь на своём рисунке, у меня О-точка пересечения диагоналей ромба): AO= =
Теперь перемножим диагонали (9*2* 24) и получим ответ.
Дан параллелограмм ABCD с длинами сторон 12 и 8. Биссектрисы его углов при пересечении образуют четырехугольник. Чему равна длина диагоналей этого четырехугольника?
По свойству параллельных прямых и секущей сумма углов при одной стороне параллелограмма равна 180°. Следовательно, биссектрисы его соседних углов пересекаются под прямым углом. Поэтому четырехугольник, образованный четырьмя биссектрисами параллелограмма - прямоугольник. Обозначим его вершины К, L, M и N.
Биссектрисы параллелограмма, являясь секущими, отсекают от него равнобедренные треугольники ( они делят углы пополам, и накрестлежащие углы тоже равны). Противоположные стороны параллелограмма равны =>
АВ=BQ=AT=CD=CR=DS=8 Тогда ВR=12-CR=4. Аналогично длина отрезков QC,, DT,, AS равна 4.
Отрезки QR и TS равны 12-2•4=4.
По 1-му признаку равенства треугольников ∆ АВТ=∆ RCD и ∆ ABQ=∆ СDS ⇒ их стороны и углы, заключённые между ними, равны.
В равнобедренном треугольнике биссектриса=высота=медиана. ⇒ BL=LT=RN=ND
Биссектрисы противоположных углов параллелограмма параллельны: ВТ║RD, а BR║TD как лежащие на параллельных сторонах ABCD.
Из доказанного выше BL=RN. ⇒ BL=RN. ⇒
Четырехугольник BRNL – параллелограмм, ⇒LN=BR=4
LN - диагональ прямоугольника KLMN. Диагонали прямоугольника равны.
КМ=LN=4 (ед. длины)
Подробнее - на -
Объяснение:
1) Ну чертить тебе придётся самому. там не сложно. Сначала окружность, потом внутри неё чертишь произвольный четырёхугольник. Даже с разными длинами сторон, по условию не указано, что правильный. Потом пятиугольник
2) Площадь прямоугольника (обозначается буквой S) равняется произведению двух сторон, имеющих общий угол. То бишь нижнюю или верхнюю умножь на боковую. То бишь S=5*8=40 (см2)
3) Площадь параллелограмма равна длине основания умноженной на высоту. S=6*9=54 (см2)
4) Это можно нагуглить за 10 секунд. Не спрашивай откуда узнал) 900 градусов.
5) Площадь треугольника равняется высоте умноженной на сторону, к которой она проведена. Т.к площадь равна 36, а сторона 6, то высота равна 36/6=6 (см)
6) Площадь трапеции равняется сумме оснований (верхняя и нижняя сторона) поделённой на два, после чего умноженной на высоту.
Значит сторона (обозначим её АВ) равна: АВ=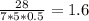
(см)
0.5 тут играет роль деления на два, т.к умножение на 0.5, она же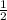
это то же самое, что деление на 2.
7) 1)Находим площадь исходного прямоугольника по формуле из второй задачи (перемножь две стороны, чтобы не умножать число на десятичную дробь переведи дециметры в сантиметры, для этого нужно умножить на 10, т.к 1 дм=10 см. Получится 40 и 32 см).
2)Потом находим площадь одного такого квадрата, умножив 0.2 на 0.2, т.к у квадрата стороны равны. Тут та же история, переводи в сантиметры.
3) делим площадь всего прямоугольника на площадь квадрата и получаем количество квадратов.
4) ???
5) Профит. Попробуй посчитать сам, у тебя получится.
8) Тут уже поинтереснее. Делай рисунок.
Площадь ромба можно двумя перемножив основание на высоту, либо перемножив две диагонали друг на друга, после чего разделив полученное число на два. Пойдём по второму
У ромба все стороны равны, т.е все четыре равны 15 см. А вот диагонали разные. Одна у нас есть и равна 24 см. Диагонали ромба пересекаются под прямым углом, а это значит, что у нас есть прямоугольный треугольник в котором мы знаем 2 стороны. По теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы) найдём половинку второй диагонали. Тут нужен рисунок, но заливать картинку мне лень, извини)
Поэтому объясню на словах, а там тащи сам. Запоминай: в прямоуг. треугольнике катетами называются стороны, которые расходятся из прямого угла, то бишь если сторона в таком треугольнике соприкасается с прямым углом, то это катет. Гипотенуза не соприкасается с прямым углом. В нашем случае (ты увидишь это, когда нарисуешь ромб с диагоналями) под прямым углом по свойству ромба пересекаются его диагонали. Значит, чтобы найти половинку второй диагонали мы рассмотрим треугольник, у которого 2 стороны - это половинки диагоналей, а вторая - любая сторона ромба. Ромб состоит из 4 таких треугольников.
По т. Пифагора сумма квадратов катетов (половинки диагоналей) равна квадрату гипотенузы (сторона ромба), значит:
Половинка диагонали в квадрате равна квадрат гипотенузы минус квадрат известного катета. Полученное значение ставим под корень и находим половинку диагонали уже НЕ в квадрате:
Выглядеть это будет как-то так (буквы сам поставишь на своём рисунке, у меня О-точка пересечения диагоналей ромба): AO=
= 
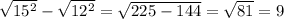
Теперь перемножим диагонали (9*2* 24) и получим ответ.
Дальше я всё, устал.