Объяснение: так там угол в 60 а сумма дополнительных углов 180 то соседний равен <CDA= 120 и так это ромб <ВAD=60 градусам так как диагональ BD делит углы B и D пополам а так же делит на два равносторонних треугольника BAD и BCD то диагональ BD равна 8 , теперь вычислим площадь ромба по формуле ab*sinL так как стороны равны sinL не важно какой угол мы возьмем sin120 или sin 60 они равны но если вы не формулу суммы углов то лучше использовать sin60 и мы вычисляем *sin60= *64= 32
На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM=СP, BN=DQ, BM=DP, NC=QA. Докажите, что ABCD, MNPQ - параллелограммы.
***
Обозначим равные отрезки одинаковыми буквами:
АМ=СР=а
BN=DQ=b
BM=DP=c
NC=QA=d
АВ=а+с
СD=a+c ⇒ AB=CD
BC=b+d
AD=b+d ⇒ BC=AD
В четырехугольнике АВСD противоположные стороны попарно равны. ⇒
АВСD - параллелограмм ( 2-й признак)
–––––––––––––––––––––
Рассмотрим ∆ MBN и ∆ PDQ
∠ А=∠С как противоположные углы параллелограмма АВСD.
Содержащие эти углы стороны равны по условию ⇒
∆ MBN = ∆ PDQ по 1-му признаку.⇒ MN=PQ
Аналогично доказывается равенство сторон MQ и NP
В четырехугольнике MNРQ противоположные стороны равны ⇒ MNРQ - параллелограмм.
ответ:32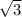
Объяснение: так там угол в 60 а сумма дополнительных углов 180 то соседний равен <CDA= 120 и так это ромб <ВAD=60 градусам так как диагональ BD делит углы B и D пополам а так же делит на два равносторонних треугольника BAD и BCD то диагональ BD равна 8 , теперь вычислим площадь ромба по формуле ab*sinL так как стороны равны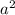
sinL не важно какой угол мы возьмем sin120 или sin 60 они равны но если вы не формулу суммы углов то лучше использовать sin60 и мы вычисляем 
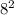*sin60= 
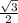*64= 32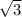
На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM=СP, BN=DQ, BM=DP, NC=QA. Докажите, что ABCD, MNPQ - параллелограммы.
***
Обозначим равные отрезки одинаковыми буквами:
АМ=СР=а
BN=DQ=b
BM=DP=c
NC=QA=d
АВ=а+с
СD=a+c ⇒ AB=CD
BC=b+d
AD=b+d ⇒ BC=AD
В четырехугольнике АВСD противоположные стороны попарно равны. ⇒
АВСD - параллелограмм ( 2-й признак)
–––––––––––––––––––––
Рассмотрим ∆ MBN и ∆ PDQ
∠ А=∠С как противоположные углы параллелограмма АВСD.
Содержащие эти углы стороны равны по условию ⇒
∆ MBN = ∆ PDQ по 1-му признаку.⇒ MN=PQ
Аналогично доказывается равенство сторон MQ и NP
В четырехугольнике MNРQ противоположные стороны равны ⇒ MNРQ - параллелограмм.