3.диагональ боковой грани правильной треугольной призмы образует с основанием угол, равный 30°. найдите объем призмы, если площадь боковой поверхности призмы равна 72 корней из 3 см^2.
Дано: ΔABC - прямоугольный, ∠C = 90°, ∠ABC = 60°, AC = 6 см.
Найти: а) AB; б) CD
Решение: 1) Рассмотрим ΔABC: ∠ABC = 60°, ∠C = 90°, ∠A = 30° (т. к. 180° - (90° + 60°) = 30); Найдем сторону AB через синус угла ABC (синус острого угла равен отношению противолежащего катета к гипотенузе): sin60° = = = ; Отсюда AB = = см.
2) Рассмотрим ΔACD, в котором ∠D = 90°, а ∠CAD = 30° (из 1); Согласно свойству прямоугольного треугольника с углом в 30°, катет, лежащий напротив угла в 30°, равен половине гипотенузы, следовательно, CD = 1/2*AC = 1/2*6 = 3 см.
Вписанные углы опирающиеся на диаметр равны по 90°, поэтому ∠ADC=90°=∠CBA.
Треугольник ADC - равнобедренный (DA=DC) и прямоугольный (∠ADC=90°), поэтому углы при его основании равны по 45°. ∠DAC=45°=∠DCA
Треугольник ABC - прямоугольный (∠CBA=90°), так же 2AB=AC. Угол лежащий напротив катета, который вдвое меньше гипотенузы равен 30°, поэтому ∠BCA=30°. Сумма острых углов в прямоугольном треугольнике составляет 90°, поэтому ∠BАС=60°.
Дано: ΔABC - прямоугольный, ∠C = 90°, ∠ABC = 60°, AC = 6 см.
Найти: а) AB; б) CD
Решение: 1) Рассмотрим ΔABC: ∠ABC = 60°, ∠C = 90°, ∠A = 30° (т. к. 180° - (90° + 60°) = 30); Найдем сторону AB через синус угла ABC (синус острого угла равен отношению противолежащего катета к гипотенузе): sin60° =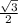 =
= 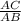 =
= 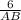 ; Отсюда AB =
; Отсюда AB = 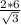 =
= 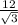 см.
см.
2) Рассмотрим ΔACD, в котором ∠D = 90°, а ∠CAD = 30° (из 1); Согласно свойству прямоугольного треугольника с углом в 30°, катет, лежащий напротив угла в 30°, равен половине гипотенузы, следовательно, CD = 1/2*AC = 1/2*6 = 3 см.
ответ: а)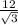 см; б) CD = 3 см.
см; б) CD = 3 см.
Вписанные углы опирающиеся на диаметр равны по 90°, поэтому ∠ADC=90°=∠CBA.
Треугольник ADC - равнобедренный (DA=DC) и прямоугольный (∠ADC=90°), поэтому углы при его основании равны по 45°. ∠DAC=45°=∠DCA
Треугольник ABC - прямоугольный (∠CBA=90°), так же 2AB=AC. Угол лежащий напротив катета, который вдвое меньше гипотенузы равен 30°, поэтому ∠BCA=30°. Сумма острых углов в прямоугольном треугольнике составляет 90°, поэтому ∠BАС=60°.
∠BAD = ∠BAC+∠DAC = 60°+45° = 105°
∠BCD = ∠BCA+∠DCA = 30°+45° = 75°
ответ: ∠BAD=105°; ∠BСD=75°.