Найдём критические точки (это те значения в которых производная функции равна нулю или не имеет значений (к примеру 1/x, при x=0 функция не имеет значения), они называются точками разрыва).
Сразу видно что у функции нет точек разрыва (то есть она определена на всей числовой прямой), поэтому просто приравняем производную функции к нулю:
[Производная степенной функции: ]
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
3x=0 или x+2=0
x=0 или x=-2
Итого у нас 2 точки экстремума.
Теперь посмотрим как ведёт себя производная функции между ними. Там, где производная принимает положительные значения, сама функция возрастает, там где отрицательные - убывает.
(Рисунок)
Как видно из рисунка, функция возрастает на промежутке (-∞;-2)U(0;+∞) и убывает на (-2;0)
Объяснение:
Найдём критические точки (это те значения в которых производная функции равна нулю или не имеет значений (к примеру 1/x, при x=0 функция не имеет значения), они называются точками разрыва).
Сразу видно что у функции нет точек разрыва (то есть она определена на всей числовой прямой), поэтому просто приравняем производную функции к нулю:
[Производная степенной функции: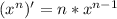 ]
]
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
3x=0 или x+2=0
x=0 или x=-2
Итого у нас 2 точки экстремума.
Теперь посмотрим как ведёт себя производная функции между ними. Там, где производная принимает положительные значения, сама функция возрастает, там где отрицательные - убывает.
(Рисунок)
Как видно из рисунка, функция возрастает на промежутке (-∞;-2)U(0;+∞) и убывает на (-2;0)
Точки экстремума:
-6 ; 0
Монотонность функции:
функция возрастает на промежутке (-∞;-2)U(0;+∞)
функция убывает на промежутке (-2;0)
ответ:Треугольник RFE равен треугольнику ЕFS
Оба эти треугольника прямоугольные,по четвёртому признаку равенства прямоугольных треугольников-по гипотенузе и по острому углу,они равны
EF-общая сторона,она же гипотенуза
<SEF=<REF ,по условию задачи
Номер 2
Треугольник АDE равен треугольнику FMB
Данные треугольники прямоугольные,они равны по 4 признаку равенства прямоугольных треугольников -по гипотенузе и острому углу
AD=FB по условию задачи
<А=<В, т к треугольник АСВ равнобедренный,а углы при основании равнобедренного треугольника равны между собой
А равнобедренный,т к
АD=FB;DC=CF; по условию задачи
Объяснение: