5. Точки О(0; 0), А(х; у), B(6; 8) и C(0; 6) являются вершинами па-
раллелограмма. Найдите координаты точки А:
А)(2;6)
В)(2;4)
С)(6;2)
Д)(6;0)

Показать ответ

Ответ:

Laurahsnbrg

13.08.2021 21:24

ВD - биссектриса и делит угол В на две равные части, поэтому дуги АD и СD, на которые опираются половины вписанного угла В, равны.
По условию АD =АС .
Треугольник АСD равнобедренный. ∠ АСD=∠ АDС.
АС=АD равные хорды и стягивают равные дуги.
Значит, дуга АВС=дуге АD.
Но ◡АD=◡СD как дуги, на которые опираются равные углы АВD и СВD ⇒
Точки А, С, D делят окружность на три равные дуги с градусной мерой 360º:3=120º
Вписанный угол АВС опирается на дугу АDС=120º*2=240º Вписанный угол равен половине дуги, на которую опирается. ⇒
Угол АВС=240º: 2=120º
Продолжение биссектрисы угла b треугольника авс пересекает описанную около треугольника окружность в

Продолжение биссектрисы угла b треугольника авс пересекает описанную около треугольника окружность в

0,0(0 оценок)

Ответ:

val40

20.01.2022 13:00

Дано :

ΔАВС ~ ΔA₁В₁С₁.

Отношение сходственных сторон = $\frac{6}{5}$ .

S(ΔАВС) = S(ΔА₁В₁С₁) + 77 (см²).

Найти :

S(ΔАВС) = ?

S(ΔА₁В₁С₁) = ?

Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.

Отсюда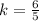 $k = \frac{6}{5}$ .

Так как k > 1, то в числителе стоит бо́льший треугольник.

Площади подобных треугольников относятся как квадрат коэффициента подобия.

Пусть S(ΔА₁В₁С₁) = х, тогда S(ΔАВС) = х + 77 (см²) (так как площадь ΔАВС больше площади ΔА₁В₁С₁, то он, как раз таки, и есть бо́льший треугольник).

Составим уравнение -

$\frac{S(\triangle ABC)}{S(\trianle A_{1} B_{1}C_{1})} = k^{2}\\\\ \frac{x + 77}{x} = (\frac{6}{5})^{2}\\\\\frac{x + 77}{x} = \frac{36}{25}\\\\25*(x + 77) = 36x\\\\25x + 1925 = 36x\\\\25x - 36x = -1925\\\\-11x = -1925\\\\ \boxed{x = 175}$